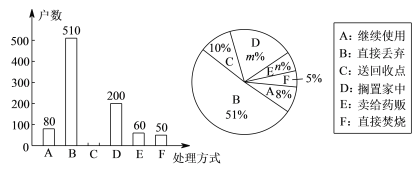��Ŀ����
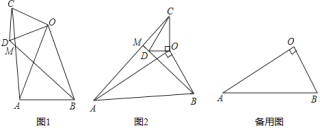
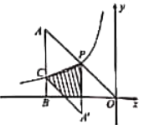
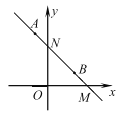
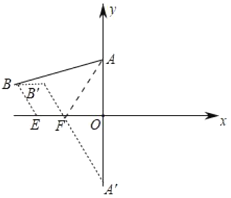
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ�����ֱ�����ǰ�ABC���ڵڶ����ޣ�б�������������ϣ���C����Ϊ����1��0����tan��ACO��2��һ�κ���y��kx+b��ͼ����B��C������������y��![]() ��ͼ����B��
��ͼ����B��
��1����һ�κ�����ϵʽ�ͷ����������Ĺ�ϵʽ��
��2����x��0ʱ��kx+b��![]() ��0�Ľ⼯Ϊ�� ����
��0�Ľ⼯Ϊ�� ����
��3����x����������E��F����E�ڵ�F����ߣ���EF��1�����ı���ABEF�ܳ���Сʱ����ֱ��д����E�ĺ�����Ϊ�� ����
���𰸡���1��y����![]() x��
x��![]() ��y����
��y����![]() ����2����3��x��0����3��-
����2����3��x��0����3��-![]()
��������
��1������B��BF��x���ڵ�F���ɡ�AOC�ա�CFB��õ�B�����꣬���ô���ϵ���������һ�κ����ͷ����������Ĺ�ϵʽ��
��2����x��0ʱ�����һ�κ���ֵy��kx��bС�ڷ���������y��![]() ��x��ȡֵ��Χ�����ͼ�μ���ֱ��д���𰸣�
��x��ȡֵ��Χ�����ͼ�μ���ֱ��д���𰸣�
��3����B����ƽ��1����λ�õ�B�䣨2��1��������A����x��ĶԳƵ�A�䣨0��2��������A��B�佻x���ڵ�F�����ֱ��A��B��Ľ���ʽ�����F�����꼴�ɽ�����⣮
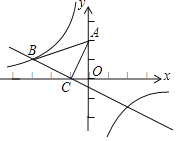
�⣺��1����ͼ1�У�����B��BF��x���ڵ�F��

����C��������1��0����
��OC��1��
��tan��ACO��2��![]() ��
��
��OA��2��
���A������0��2����
��OA��2��OC��1��
�ߡ�BCA��90����
���BCF+��ACO��90����
���ߡ�CAO+��ACO��90����
���BCF����CAO��
���AOC�ա�CFB��AAS����
��FC��OA��2��BF��OC��1��
����B����������3��1����
����B��������뷴������������ʽ�ɵã�1��![]() ����ã�m����3��
����ã�m����3��
�ʿɵ÷�������������ʽΪy����![]() ��
��
����B��C���������һ�κ�������ʽ�ɵã�
![]() ����ã�
����ã� 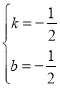 ��
��
�ʿɵ�һ�κ�������ʽΪy����![]() x��
x��![]() ��
��
��2����ϵ�B�����꼰ͼ�ɵõ�x��0ʱ��kx+b��![]() ��0�Ľ⼯Ϊ����3��x��0��
��0�Ľ⼯Ϊ����3��x��0��
�ʴ�Ϊ����3��x��0��
��3����ͼ�У���span>B����ƽ��1����λ�õ�B�䣨2��1��������A����x��ĶԳƵ�A�䣨0��2��������A��B�佻x���ڵ�F��
��ֱ��A��B��Ľ���ʽΪax+b��a��0��
��A�䣨0��2����B�䣨2��1�������![]()
���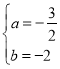
��ֱ��A��B��Ľ���ʽΪy��![]() x2��
x2��
����y=0����![]() x2=0
x2=0
���x=-![]()
��F��![]() ��0����
��0����
��OF��![]()
��OE��1��![]() ��
��![]()
���E�ĺ�����Ϊ![]() ��
��
�ʴ�Ϊ![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ�������������ļӿ��Լ������ֻ����ռ������������ΪԽ��Խ���û��IJ�������ϰ�ߣ��ɴ˴�����һ���������ƽ̨����֪ij����ƽ̨���Ͳͷ������Ͳ;����йأ���ƽֻ̨��5ǧ��Χ�����ͣ���Ϊ�����Ͳ�Ա���Ͳ����룬�ִӸ�ƽ̨�����ȡ80�����������û�����ͳ�ƣ����Ͳ;������ͳ�ƽ�����±���
�Ͳ;���x��ǧ�ף� | 0 | 1 | 2 | 3 | 4 |
���� | 12 | 20 | 24 | 16 | 8 |
��1������80�����������û�����ȡһ���û������û����Ͳ;��벻����3ǧ�ĸ���Ϊ ��
��2������80���û��Ͳ;���Ϊ������ͬһ������ȡ��С�����ݵ��м�ֵ������ڶ�С�飨1��x ��2�����м�ֵ��1.5�����Թ������ø�ƽ̨�������û���ƽ���Ͳ;��룻
��3����������ƽ̨���Ͳ�Ա���Ͳͷ������Ͳ;����йأ�������2ǧ��ʱ��ÿ��3Ԫ������2ǧ������4ǧ��ʱ��ÿ��5Ԫ������4ǧ��ʱ��ÿ��9Ԫ�� �Ը���80���û������Ͳͷ��õ�ƽ����Ϊ���ݣ����Ͳ�Աһ���Ŀ�����벻����150Ԫ���Թ���һ������Ҫ�Ͷ��ٷ�������