��Ŀ����
����Ŀ����Rt��ACB��Rt��AEF�У���ACB����AEF��90��������P��BF���е㣬����PC��PE��
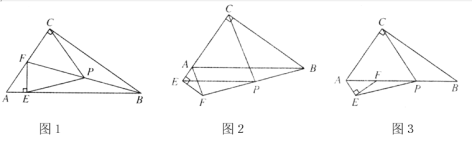
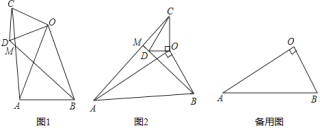
(1) ��ͼ1������E��F�ֱ����ڱ�AB��AC�ϣ���֤��PC��PE��
(2) ��ͼ2����ͼ1�еġ�AEF���ŵ�A˳ʱ����ת������E���ڱ�CA���ӳ�����ʱ��̽��PC��PE��������ϵ����˵�����ɣ�
(3) ��ͼ3����ͼ2�еġ�AEF���ŵ�A˳ʱ����ת����F���ڱ�AB�ϣ������������䣬����(2)�еĽ����Ƿ����仯��������䣬�����֤��������仯����˵�����ɣ�
���𰸡���1������������2��PC��PE�����ɼ���������3�����������ɼ�����
��������
��1������ֱ��������б�ߵ����ߵ���б�ߵ�һ�룬���ɣ�
��2�����жϡ�CBP�ա�HPF��������ֱ��������б�ߵ����ߵ���б�ߵ�һ�룻
��3�����жϡ�DAF�ա�EAF�����жϡ�DAP�ա�EAP��Ȼ���ñ���ʽ���ɣ�
�⣺��1��֤������ͼ��
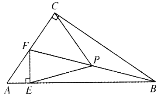
�ߡ�ACB����AEF��90����
���FCB����BEF��Ϊֱ�������Σ�
����P��BF���е㣬
��CP��![]() BF��EP��
BF��EP��![]() BF��
BF��
��PC��PE��
��2��PC��PE�������£�
��ͼ2���ӳ�CP��EF���ڵ�H��
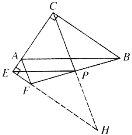
�ߡ�ACB����AEF��90����
��EH//CB��
���CBP����PFH����H����BCP��
����P��BF���е㣬
��PF��PB��
���CBP�ա�HFP(AAS)��
��PC��PH��
�ߡ�AEF��90����
����Rt��CEH��EP��![]() CH��
CH��
��PC��PE��
��3��(2)�еĽ��ۣ���Ȼ��������PC��PE���������£�
��ͼ3������F��FD��AC�ڵ�D������P��PM��AC�ڵ�M������PD��
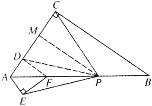
�ߡ�DAF����EAF����FDA����FEA��90����
����DAF����EAF��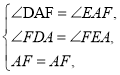
���DAF�ա�EAF(AAS)��
��AD��AE��
����DAP�ա�EAP�У�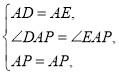
���DAP�ա�EAP (SAS)��
��PD��PF��
��FD��AC��BC��AC��PM��AC��
��FD//BC//PM��
��![]() ��
��
����P��BF���е㣬
��DM��MC��
����PM��AC��
��PC��PD��
�֡�PD��PE��
��PC��PE��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�