Question

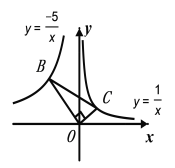
【题目】如图，点B、C分别在反比例函数y=和y=上，连接OB，OC，BC且OB⊥OC，则的值为（ ）

A.5B.1C.D.

Answer 1

【答案】C

【解析】

过B点向x轴作垂线交x轴于点D，过C点向x轴作垂线交x轴于点E，证明△BOD∽△COE，根据k的几何意义可得出S△BOD和S△COE，根据面积比等于相似比的平方即可得出答案．

解：过B点向x轴作垂线交x轴于点D，过C点向x轴作垂线交x轴于点E，

∵BD⊥x轴，CE⊥x轴，

∴∠BDO=∠CEO=90°，

∵OB⊥OC，

∴∠BOD+∠COE=90°，

∵∠DBO+∠BOD=90°，

∴∠DBO=∠COE，

∴△BOD∽△COE，

∴，

由k的几何意义可知S△BOD=5，S△COE=1，

∴=5，

∴=，

故选：C．