题目内容
【题目】小明在课外研究中,设计如下题目:直线![]() 过点
过点![]() ,
,![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
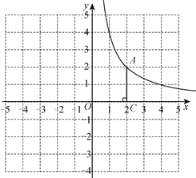
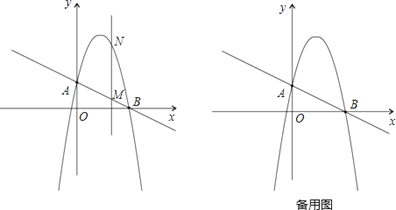
(1)求直线和曲线的关系式.(图1)
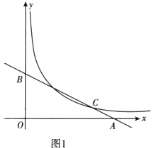
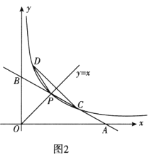
(2)小明发现曲线![]() 关于直线
关于直线![]() 对称,他把曲线
对称,他把曲线![]() 与直线
与直线![]() 的交点
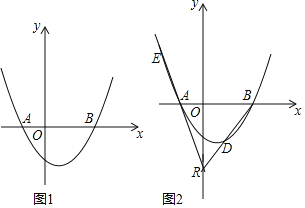
的交点![]() 叫做曲线的顶点.(图2)
叫做曲线的顶点.(图2)
①直接写出![]() 点的坐标;
点的坐标;
②若点![]() 从
从![]() 点出发向上运动,运动到
点出发向上运动,运动到![]() 时停止,求此时
时停止,求此时![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②
,②![]() .
.
【解析】
(1)把![]() ,
,![]() 代入
代入![]() ,列出关于k和b的二元一次方程组,求出k和b的值,即可求出直线
,列出关于k和b的二元一次方程组,求出k和b的值,即可求出直线![]() 的解析式,把点
的解析式,把点![]() 代入直线解析式,求出n=1,把
代入直线解析式,求出n=1,把 ![]() 代入
代入![]() ,即可求出曲线的解析式.
,即可求出曲线的解析式.
(2)列方程组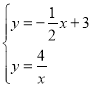 ,方程组的解,即为P点的坐标,由曲线
,方程组的解,即为P点的坐标,由曲线![]() 关于直线
关于直线![]() 对称,
对称,![]() ,可得点C和点D 关于
,可得点C和点D 关于![]() 对称,解点D的坐标,通过做辅助线,分别过点D、点P、点C向x轴作垂线,分别交x轴于点M、点N、点F,得到
对称,解点D的坐标,通过做辅助线,分别过点D、点P、点C向x轴作垂线,分别交x轴于点M、点N、点F,得到![]() ,求得
,求得![]() 的面积.
的面积.
(1)将点![]() ,
,![]() 的坐标代入
的坐标代入![]() ,
,
得:![]() ,解得
,解得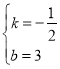
∴直线解析式为:![]() ,
,
∵直线![]() 过点
过点![]()
∴把C点坐标代入![]() 得,n=1,
得,n=1,
∴C点坐标为![]() ,
,
将C点坐标代入![]() ,解得m=4,
,解得m=4,
∴曲线的关系式为:![]() .
.
(2) ①∵点P是曲线![]() 与直线
与直线![]() 的交点,
的交点,
∴得到方程组![]() ,解得,
,解得,![]() 或
或![]() ,
,
∵x>0,
∴P点的坐标为![]()
②分别过点D、点P、点C向x轴作垂线,分别交x轴于点M、点N、点F.
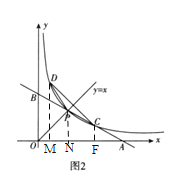
∵曲线![]() 关于直线
关于直线![]() 对称,
对称,
∴当![]() 时,点C和点D 关于
时,点C和点D 关于![]() 对称,
对称,
∴点D得坐标为(1,4),
∴![]()
![]() ,
,
∴![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目