题目内容
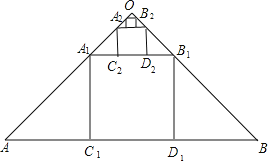
【题目】如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3;……;依次作下去,则第n个正方形AnBnCnDn的边长是________.
【答案】![]()
【解析】
过O作OM垂直于AB,交AB于点M,交A1B1于点N,由三角形OAB与三角形OA1B1都为等腰直角三角形,得到M为AB的中点,N为A1B1的中点,根据直角三角形斜边上的中线等于斜边的一半可得出OM为AB的一半,由AB=1求出OM的长,再由ON为A1B1的一半,即为MN的一半,可得出ON与OM的比值,求出MN的长,即为第1个正方形的边长,同理求出第2个正方形的边长,依此类推即可得到第n个正方形的边长.
解:过O作OM⊥AB,交AB于点M,交A1B1于点N,如图所示: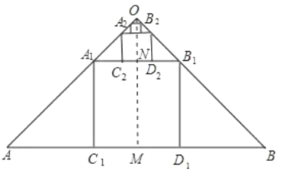
∵正方形A1B1C1D1,
∴A1B1∥AB,∴ON⊥A1B1,
∵△OAB为斜边为1的等腰直角三角形,
∴OM=![]() AB=
AB=![]() ,
,
又∵△OA1B1为等腰直角三角形,
∴ON=![]() A1B1=
A1B1=![]() MN,
MN,
∴ON:OM=1:3,
∴ON=![]() OM=
OM=![]() ,
,
∴第1个正方形的边长A1C1=MN=![]() OM=
OM=![]() ×
×![]() =
=![]() ,
,
同理第2个正方形的边长A2C2=![]() ON=
ON=![]() ×
×![]() =
=![]() ,
,
则第n个正方形AnBnDnCn的边长![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目