题目内容
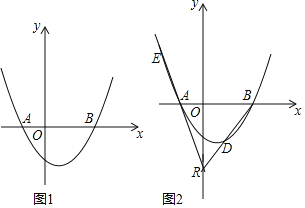
【题目】如果抛物线C1的顶点在抛物线C2上,抛物线C2的顶点也在抛物线C1上,那么我们称抛物线C1与C2为“互相关联”的抛物线.如图,已知抛物线![]() 与
与![]() 是“互相关联”的抛物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,-1).
是“互相关联”的抛物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,-1).
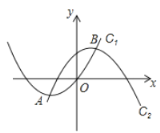
(1)直接写出点A,B的坐标和抛物线C2的解析式.
(2)抛物线C2上是否存在点E,使得△ABE是以AB为直角边的直角三角形?如果存在,请求出点E的坐标;如果不存在,请说明理由.
【答案】(1)A(-2,-1),B(2,3),![]() ;(2)存在,E的坐标为(6,-1)或(10,-13).
;(2)存在,E的坐标为(6,-1)或(10,-13).
【解析】
(1)由抛物线![]() 可得A(-2,-1),将
可得A(-2,-1),将![]() ,D(6,-1)代入C2:y2=ax2+x+c,求得y2=-
,D(6,-1)代入C2:y2=ax2+x+c,求得y2=-![]() x2+x+2,B(2,3).
x2+x+2,B(2,3).
(2)易得直线AB的解析式:![]() ,若B为直角顶点,
,若B为直角顶点,![]() ,E(6,-1);若A为直角顶点,
,E(6,-1);若A为直角顶点,![]() ,E(10,-13).
,E(10,-13).
(1)由抛物线![]() 可得
可得
A(-2,-1)
由抛物线C2:y2=ax2+x+c过点A,D(6,-1)
得![]()
解得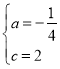
故抛物线C2的解析式为y2=-![]() x2+x+2.
x2+x+2.
∵y2=-![]() x2+x+2.
x2+x+2.
=![]() (x-2)2+3,
(x-2)2+3,
∴点B的坐标为(2,3).
(2)存在.
设点E的坐标为(m,![]() m2+m+2).
m2+m+2).
∵A(-2,-1),B(2,3),
∴AB2=(2+2)2+(3+1)2=32,
AE2=(m+2)2+(![]() m2+m+2+1)2,
m2+m+2+1)2,
BE2=(m-2)2+(m2+m+2-3)2.
①当点A为直角顶点时,有AB2+AE2=BE2,
即32+(m+2)2+(![]() m2+m+2+1)2
m2+m+2+1)2
=(m-2)2+(![]() m2+m+2-3)2,
m2+m+2-3)2,
解得m1=-2(不合题意,舍去),m2=10,
∴E(10,-13).
②当点B为直角顶点时,有AB2+BE2=AE2,
即32+(m-2)2+(![]() m2+m+2-3)2
m2+m+2-3)2
=(m+2)2+(![]() m2+m+2+1)2,
m2+m+2+1)2,
解得m3=6,m4=2(不合题意,舍去),
∴E(6,-1).
综上所述,当E的坐标为(6,-1)或(10,-13).