题目内容
【题目】如图,已知抛物线y=![]() x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.

【答案】(1)m=1,n=![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】分析:(1)由点C的坐标利用待定系数法即可求出一次函数解析式中的常数项b,再令一次函数解析式中y=0求出x值,由此可得出点B的坐标,由点B、C的坐标利用待定系数法即可求出二次函数解析式中的系数m、n;
(2)过点C作CF⊥x轴于点F,过点A作AG⊥BC于点G,由二次函数解析式可求出交点A、B的坐标,由点B、C、A点的坐标,可找出线段CF、BF、AF、BA的长,通过解直角三角形即可找出BG、AG、BC的长,再根据正切的计算公式即可得出结论;
(3)假设存在,连接AE,过点E作EM⊥x轴于点M,通过角的计算得出∠BAE=∠BDE=∠BCA,设出点E的坐标,根据(2)的结论tan∠ACB=![]() ,即可得出关于t的一元二次方程,解方程即可得出结论.
,即可得出关于t的一元二次方程,解方程即可得出结论.
详解:(1)∵直线y=x+b经过点C(5,6) ∴b=1
∵B在x轴上,且在直线y=x+b上 ∴B(1,0)
∵抛物线y=![]() x2+mx+n过B(1,0)、C(5,6)
x2+mx+n过B(1,0)、C(5,6)
∴ m=1,n=![]()
(2)作CF⊥x轴于F,作AG⊥BC于G
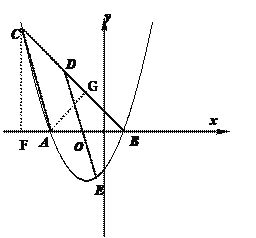
∴F(5,0)
∵抛物线y=![]() x2+mx+n与x轴交于A、B
x2+mx+n与x轴交于A、B
∴A(3,0) B(1,0)∴CF=BF=6,AF=2,AB=4∴∠CBF=45°,BC=6![]() ,
,
∴BG=AG=2![]() ∴CG=4
∴CG=4![]()
∴tan∠ACB=![]()
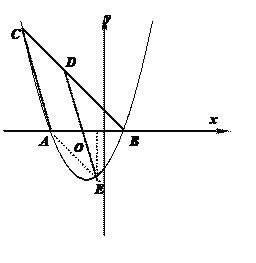
(3) ∵DE∥AC ∴∠BDE=∠BCA∵∠DEA=45° ∠DBA=45°
∴∠BAE=∠BDE=∠BCA
∴tan∠BAE=![]()
设E(t, ![]() t2+t
t2+t![]() ) ∴tan∠BAE=
) ∴tan∠BAE=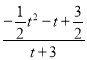 =
=![]()
∴t=0 ∴E(0, ![]() ) ∴AE=
) ∴AE=![]()

 阅读快车系列答案
阅读快车系列答案