题目内容
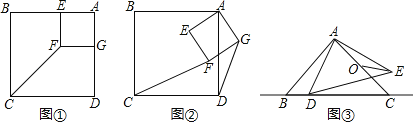
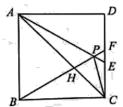
【题目】如图,在正方形ABCD中,![]() 是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC、CP、AC与BF相交于点H,下列结论中错误的是( )
是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC、CP、AC与BF相交于点H,下列结论中错误的是( )
A.AE=2DEB.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
A.利用直角三角形30度角的性质即可解决问题.
B.根据两角相等两个三角形相似即可判断.
C.通过计算证明∠DPB≠∠DPF,即可判断.
D.利用相似三角形的性质即可证明.
解:∵四边形ABCD是正方形,
∴∠D=∠DAB=90°,
∵△ABP是等边三角形,
∴∠PAB=∠PBA=∠APB=60°,
∴∠DAE=30°,
∴AE=2DE,故A正确;
∵AB∥CD,
∴∠CFP=∠ABP=∠APH=60°,
∵∠PHA=∠PBA+∠BAH=60°+45°=105°,
又∵BC=BP,∠PBC=30°,
∴∠BPC=∠BCP=75°,
∴∠CPF=105°,
∴∠PHA=∠CPF,又易得∠APB=∠CFP=60°,
∴△CFP∽△APH,故B正确;
∵∠CPB=60°+75°=135°≠∠DPF,
∴△PFC与△PCA不相似,故C错误;
∵∠PCH=∠PCB-∠BCH=75°-45°=30°,
∴∠PCH=∠PBC,
∵∠CPH=∠BPC,
∴△PCH∽△PBC,
∴![]() ,
,
∴PC2=PHPB,故D正确,
故选:C.

练习册系列答案
相关题目