题目内容
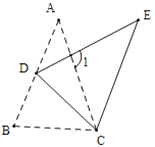
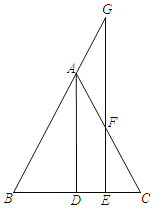
【题目】如图所示,在△ABC中,AB=AC,AD平分∠BAC,点G是BA延长线上一点,点F是AC上一点,AG=AF,连接GF并延长交BC于E.
(1)若∠B=55°,求∠AFG的度数;
(2)求证:GE⊥BC.
【答案】(1)35°;(2)见解析
【解析】
(1)利用三角形的外角的性质求出∠FAG即可解决问题.
(2)想办法证明AD∥FG即可解决问题.
(1)解:∵AB=AC,
∴∠B=∠C=55°,
∴∠GAF=∠B+∠C=110°,
∵AG=AF,
∴∠AFG=![]() (180°﹣110°)=35°.
(180°﹣110°)=35°.
(2)证明:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADC=90°
∴∠BAD=∠CAD=90°﹣55°=35°,
∴∠DAC=∠AFG,
∴AD∥FG,
∴GE⊥BC.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目