题目内容
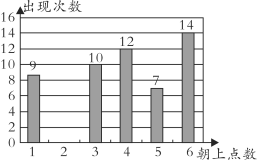
【题目】小强与小颖两位同学在学习“概率”时,做抛骰子(均匀正方体形状)试验,共随机抛了60次,出现向上点数的次数如下图所示:
(1)请补全下边的统计图;
(2)小强说:“如果抛600次,则出现向上点数为3的次数正好是100次.”他的说法正确吗?为什么?
(3)若小强与小颖各随机抛一枚骰子,求两枚骰 子向上点数之和为3的倍数的概率.
【答案】(1)见解析;(2)错误,理由见解析;(3)![]()
【解析】
(1)根据各组频数之和等于数据总数60,可求出出现向上的点数为2的次数,从而画出对应的图形;
(2)因为事件发生具有随机性,所以不能用这次试验的频率估计概率,小强的说法是错误的;
(3)可应用列表法或树形图法求出结果.
解:(1)出现向上的点数为2的次数:60-9-10-12-7-14=8,
补全统计图如下:
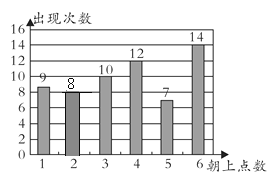
(2)小强的说法错误,因为事件发生具有随机性,故“向上点数为3”的次数不一定是100次.
(3)用a表示小强抛一枚骰子时出现向上的点数,b表示小颖抛一枚骰子时出现向上的点数,a+b表示点数和.列表如下:
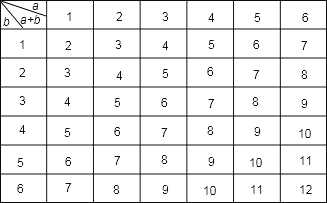
从表中可以看出,一共有36种可能的结果,其中出现向上点数之和为3的倍数的结果有12种,故P(出现向上点数之和为3的倍数)=![]() =
=![]() .
.

练习册系列答案
相关题目