题目内容
如图,在直角梯形ABCD中,AB∥CD,∠A=90°,∠B=45°,AB=4 , BC=3,F是DC上一点,且CF=
, BC=3,F是DC上一点,且CF= , E,是线段AB上一动点,将射线EF绕点E顺时针旋转45°交BC边于点G.
, E,是线段AB上一动点,将射线EF绕点E顺时针旋转45°交BC边于点G.
小题1:直接写出线段AD和CD的长;
小题2:设AE=x,当x为何值时△BEG是等腰三角形;
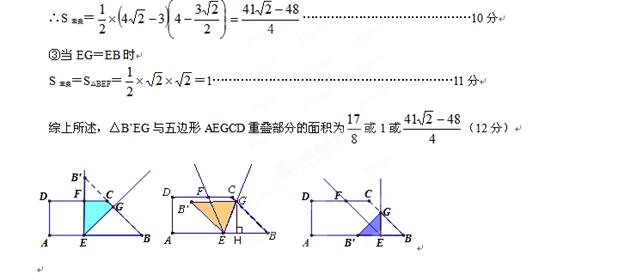
小题3:当△BEG是等腰三角形时,将△BEG沿EG折叠,得到△B’EG,求△B’EG与五边形AEGCD重叠部分的面积.
 , BC=3,F是DC上一点,且CF=
, BC=3,F是DC上一点,且CF= , E,是线段AB上一动点,将射线EF绕点E顺时针旋转45°交BC边于点G.
, E,是线段AB上一动点,将射线EF绕点E顺时针旋转45°交BC边于点G.小题1:直接写出线段AD和CD的长;
小题2:设AE=x,当x为何值时△BEG是等腰三角形;
小题3:当△BEG是等腰三角形时,将△BEG沿EG折叠,得到△B’EG,求△B’EG与五边形AEGCD重叠部分的面积.

小题1:AD=
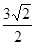 ,CD=
,CD=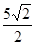
小题2:当△BEG为等腰三角形时,有三种情况
①当GE=GB时,∠GEB=∠B=45°
∵∠FEG=45°
∴∠FEB=∠FEG+∠BEG=45°+45°=90°
∴∠AEF=90°,
∵∠A=∠D=90°
易证四边形AEFD为矩形
∴AE=DF=CD-CF=
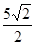 -
- =
=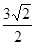 …………………………4分
…………………………4分②当BE=BG时,连结AF
 当BE=BG时,则AE=AF=3……………………………………………………6分
当BE=BG时,则AE=AF=3……………………………………………………6分③当EG=EB时
∴∠EGB=∠B=45°
∴∠GEB=90°
∵∠FEG=45°
∴∠FEB=90°+45°=135°
∴∠FEB+∠B=180°
∴FE∥BC
∵CF∥BE
∴四边形CBEF是平行四边形
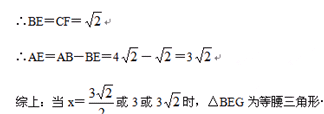
小题3:

易求得GH=
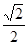 BG=
BG=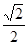 (4
(4 -3)=4-
-3)=4-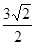
(1)利用勾股定理求出AD和CD长;
(2)分三种情况:GE=GB,BE=BG,EG=EB进行讨论;
(3)与(2)一样分三种情况进行讨论.
(2)分三种情况:GE=GB,BE=BG,EG=EB进行讨论;
(3)与(2)一样分三种情况进行讨论.

练习册系列答案
相关题目
 cm。
cm。
 中,添加下列条件不能判定平行四边形
中,添加下列条件不能判定平行四边形
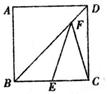
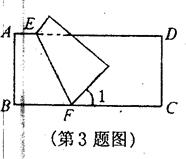
 中,点A的坐标为
中,点A的坐标为 ,点D的纵坐标为3,若将矩形沿直线AD折叠,则顶点C恰好落在边OB上E处,那么图中阴影部分的面积为( )
,点D的纵坐标为3,若将矩形沿直线AD折叠,则顶点C恰好落在边OB上E处,那么图中阴影部分的面积为( )
 、
、 是两条对角线,现从以下四个关系式 ①
是两条对角线,现从以下四个关系式 ① ,②
,② ,③
,③ ,④
,④ 中、任取一个作为条件,即可推出平行四边形
中、任取一个作为条件,即可推出平行四边形 是矩形的概率为 。
是矩形的概率为 。