题目内容
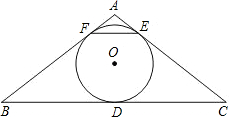
如图,⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,若AB=6,AC=5,BC=7,则AD=______,CE=______.
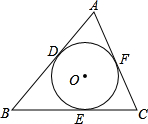

设AD=x,
∵⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,
∴AF=AD=x,
∵AB=6,AC=5,BC=7,
∴BD=BE=AB-AD=6-x,CE=CF=AC-AF=5-x,
∴6-x+5-x=7,
解得:x=2,
∴AD=2,CE=3.
故答案为:2,3.
∵⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,
∴AF=AD=x,
∵AB=6,AC=5,BC=7,
∴BD=BE=AB-AD=6-x,CE=CF=AC-AF=5-x,
∴6-x+5-x=7,
解得:x=2,
∴AD=2,CE=3.
故答案为:2,3.

练习册系列答案
相关题目