题目内容
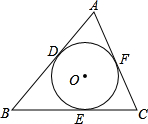
点O是△ABC内一点，且O到三边的距离相等，∠A=62°，则∠BOC=______°．
∵点O是△ABC内一点，且O到三边的距离相等，
∴O是△ABC的内切圆的圆心，
∴∠OCB=
∠ACB，∠OBC=
∠ABC，
∵∠A=62°，
∴∠ABC+∠ACB=180°-∠A=118°，
∴
（∠ACB+∠ABC）=59°，
∴∠BOC=180°-（∠OBC+∠OCB），
=180°-59°=121°．
故答案为：121．
∴O是△ABC的内切圆的圆心，
∴∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠A=62°，
∴∠ABC+∠ACB=180°-∠A=118°，
∴
| 1 |
| 2 |
∴∠BOC=180°-（∠OBC+∠OCB），
=180°-59°=121°．
故答案为：121．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
