Question

我们给出如下定义：三角形三条中线的交点称为三角形的重心．一个三角形有且只有一个重心．可以证明三角形的重心与顶点的距离等于它与对边中点的距离的两倍．
可以根据上述三角形重心的定义及性质知识解答下列问题：
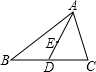
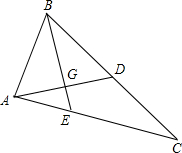
如图，∠B的平分线BE与BC边上的中线AD互相垂直，并且BE=AD=4
（1）猜想AG与GD的数量关系，并说明理由；
（2）求△ABC的三边长．

Answer 1

（1）解法1：AG=GD…（1分）
∵BE平分∠B，
∴∠ABG=∠DBG，
∵BG⊥AD，BG=BG，
∴∠BGA=∠BGD，
∴△ABG≌△DBG，
∴AG=GD，AB=BD；…（2分）
解法2：AG=GD．
∵BE平分∠B，
∴∠ABG=∠DBG，
∵BG⊥AD，BG=BG，
∴∠BGA=∠BGD，
∴△ABG≌△DBG，
∴AG=GD…（2分）

（2）解法1：如图一，延长BA到F，使AF=BA，则△BFC是等腰三角形…（4分）
∵AD是BC的中线，
∴AD是△BFC的一条中位线，
延长BE交CF于H点，则BH垂直平分FC，
∴E是△BFC的重心，…（5分）
∴AE=

1

2

EC，EH=

1

2

BE=

1

2

×4=2，
∵HC=

1

2

FC=AD=4，
∴在Rt△BHC中，BC=

BH2+HC2

=2

13

…（6分）
AB=BD=

1

2

BC=

13

…（7分）
∵在Rt△EHC中，EC=

EH2+HC2

=

22+42

=2

5

，
∴AC=AE+EC=3

5

．
解法2：如图二，从点C作CH∥AD与BE的延长线交于H…（3分）
∵GD∥HC，
∴△BGD∽△BHC
∴

BD

BC

=

BG

BH

=

GD

HC

=

1

2

，
∴D是BC的中点，G是AD的中点，也是BH的中点
∵GD=2
∴HC=4，BG=GH
设BG=x，则GE=4-x，EH=2x-4
∵AG∥HC
∴△AGE∽△CHE
∴

AG

HC

=

GE

EH

=

1

2

，即

4-x

2x-4

=

1

2

，
解出x=3…（5分）
∴在Rt△BHC中，BC=

BH2+HC2

=

62+42

=2

13

…（6分）
AB=BD=

1

2

BC=

13

，…（7分）
∵GE=1，EH=2，
∴在Rt△AGE中，AE=

AG2+GE2

=

22+12

=

5

，
∵EC=2AE=2

5

∴AC=3

5

．…（8分）