题目内容
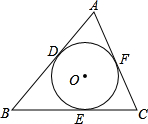
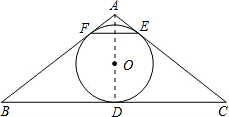
如图，在△ABC中，AB=AC，内切圆O与边BC、AC、AB分别切于D、E、F．
（1）求证：BF=CE；
（2）若∠C=30°，CE=2
，求AC．
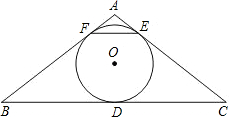
（1）求证：BF=CE；
（2）若∠C=30°，CE=2
| 3 |
（1）证明：∵AE，AF是⊙O的切线；
∴AE=AF，
又∵AC=AB，
∴AC-AE=AB-AF，
∴CE=BF，即BF=CE．
（2）连接AO、OD；
∵O是△ABC的内心，
∴OA平分∠BAC，
∵⊙O是△ABC的内切圆，D是切点，
∴OD⊥BC；
又∵AC=AB，
∴A、O、D三点共线，即AD⊥BC，
∵CD、CE是⊙O的切线，
∴CD=CE=2
，
在Rt△ACD中，由∠C=30°，CD=2
，得
AC=
=
=4．
∴AE=AF，
又∵AC=AB，
∴AC-AE=AB-AF，
∴CE=BF，即BF=CE．
（2）连接AO、OD；
∵O是△ABC的内心，
∴OA平分∠BAC，
∵⊙O是△ABC的内切圆，D是切点，
∴OD⊥BC；
又∵AC=AB，
∴A、O、D三点共线，即AD⊥BC，
∵CD、CE是⊙O的切线，
∴CD=CE=2
| 3 |
在Rt△ACD中，由∠C=30°，CD=2
| 3 |
AC=
| CD |
| cos30° |
2
| ||||
|
练习册系列答案
阅读快车系列答案
相关题目
