题目内容
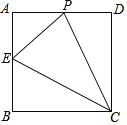
【题目】如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是_____.

【答案】3
【解析】
根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,再根据等边对等角的性质求出∠DAB=∠B,然后根据角平分线的定义与直角三角形两锐角互余求出∠B=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出BD,然后求解即可.
解:∵AD平分∠BAC,且DE⊥AB,∠C=90°,
∴CD=DE=1,
∵DE是AB的垂直平分线,
∴AD=BD,
∴∠B=∠DAB,
∵∠DAB=∠CAD,
∴∠CAD=∠DAB=∠B,
∵∠C=90°,
∴∠CAD+∠DAB+∠B=90°,
∴∠B=30°,
∴BD=2DE=2,
∴BC=BD+CD=1+2=3,
故答案为:3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A,B两类图书共1000本; 2.A类图书不少于600本; …… |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A,B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?