ЬтФПФкШн
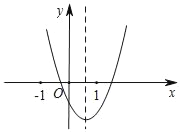
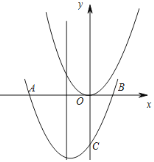
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌНЋХзЮяЯпy=x2ЦНвЦЃЌЪЙЦНвЦКѓЕФХзЮяЯпОЙ§ЕуAЃЈЈC3ЃЌ0ЃЉЁЂBЃЈ1ЃЌ0ЃЉЃЎ
(1)ЧѓЦНвЦКѓЕФХзЮяЯпЕФБэДяЪНЃЎ
(2)ЩшЦНвЦКѓЕФХзЮяЯпНЛyжсгкЕуCЃЌдкЦНвЦКѓЕФХзЮяЯпЕФЖдГЦжсЩЯгавЛЖЏЕуPЃЌЕБBPгыCPжЎКЭзюаЁЪБЃЌPЕузјБъЪЧЖрЩйЃП
(3)Шєy=x2гыЦНвЦКѓЕФХзЮяЯпЖдГЦжсНЛгкDЕуЃЌФЧУДЃЌдкЦНвЦКѓЕФХзЮяЯпЕФЖдГЦжсЩЯЃЌЪЧЗёДцдквЛЕуMЃЌЪЙЕУвдMЁЂOЁЂDЮЊЖЅЕуЕФШ§НЧаЮЁїBODЯрЫЦЃПШєДцдкЃЌЧѓЕуMзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=x2+2xЉ3ЃЛЃЈ2ЃЉЕуPзјБъЮЊЃЈЉ1ЃЌЉ2ЃЉЃЛЃЈ3ЃЉЕуMзјБъЮЊЃЈЉ1ЃЌ3ЃЉЛђЃЈЉ1ЃЌ2ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшЦНвЦКѓХзЮяЯпЕФБэДяЪНЮЊy=aЃЈx+3ЃЉЃЈx-1ЃЉЃЎгЩЬтвтПЩжЊЦНКѓХзЮяЯпЕФЖўДЮЯюЯЕЪ§гыдХзЮяЯпЕФЖўДЮЯюЯЕЪ§ЯрЭЌЃЌДгЖјПЩЧѓЕУaЕФжЕЃЌгкЪЧПЩЧѓЕУЦНвЦКѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЯШИљОнЦНвЦКѓХзЮяЯпНтЮіЪНЧѓЕУЦфЖдГЦжсЃЌДгЖјЕУГіЕуCЙигкЖдГЦжсЕФЖдГЦЕуCЁфзјБъЃЌСЌНгBCЁфЃЌгыЖдГЦжсНЛЕуМДЮЊЫљЧѓЕуPЃЌдйЧѓЕУжБЯпBCЁфНтЮіЪНЃЌСЊСЂЗНГЬзщЧѓНтПЩЕУЃЛ
ЃЈ3ЃЉЯШЧѓЕУЕуDЕФзјБъЃЌгЩЕуOЁЂBЁЂEЁЂDЕФзјБъПЩЧѓЕУOBЁЂOEЁЂDEЁЂBDЕФГЄЃЌДгЖјПЩЕУЕНЁїEDOЮЊЕШбќШ§НЧжБНЧШ§НЧаЮЃЌДгЖјПЩЕУЕНЁЯMDO=ЁЯBOD=135ЁуЃЌЙЪДЫЕБ![]() Лђ
Лђ![]() ЪБЃЌвдMЁЂOЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїBODЯрЫЦЃЎгЩБШР§ЪНПЩЧѓЕУMDЕФГЄЃЌгкЪЧПЩЧѓЕУЕуMЕФзјБъЃЎ
ЪБЃЌвдMЁЂOЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїBODЯрЫЦЃЎгЩБШР§ЪНПЩЧѓЕУMDЕФГЄЃЌгкЪЧПЩЧѓЕУЕуMЕФзјБъЃЎ
ЃЈ1ЃЉЩшЦНвЦКѓХзЮяЯпЕФБэДяЪНЮЊy=aЃЈx+3ЃЉЃЈxЉ1ЃЉЃЌ
ЁпгЩЦНвЦЕФаджЪПЩжЊдХзЮяЯпгыЦНвЦКѓХзЮяЯпЕФПЊПкДѓаЁгыЗНЯђЖМЯрЭЌЃЌ
ЁрЦНвЦКѓХзЮяЯпЕФЖўДЮЯюЯЕЪ§гыдХзЮяЯпЕФЖўДЮЯюЯЕЪ§ЯрЭЌЃЌ
ЁрЦНвЦКѓХзЮяЯпЕФЖўДЮЯюЯЕЪ§ЮЊ1ЃЌМДa=1ЃЌ
ЁрЦНвЦКѓХзЮяЯпЕФБэДяЪНЮЊy=ЃЈx+3ЃЉЃЈxЉ1ЃЉЃЌ
ећРэЕУЃКy=x2+2xЉ3ЃЛ
ЃЈ2ЃЉЁпy=x2+2xЉ3=ЃЈx+1ЃЉ2Љ4ЃЌ
ЁрХзЮяЯпЖдГЦжсЮЊжБЯпx=Љ1ЃЌгыyжсЕФНЛЕуCЃЈ0ЃЌЉ3ЃЉЃЌ
дђЕуCЙигкжБЯпx=Љ1ЕФЖдГЦЕуCЁфЃЈЉ2ЃЌЉ3ЃЉЃЌ
ШчЭМ1ЃЌ
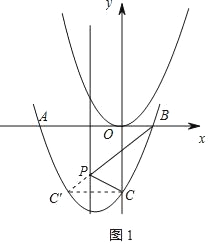
СЌНгBЃЌCЁфЃЌгыжБЯпx=Љ1ЕФНЛЕуМДЮЊЫљЧѓЕуPЃЌ
гЩBЃЈ1ЃЌ0ЃЉЃЌCЁфЃЈЉ2ЃЌЉ3ЃЉПЩЕУжБЯпBCЁфНтЮіЪНЮЊy=xЉ1ЃЌ
дђ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЫљвдЕуPзјБъЮЊЃЈЉ1ЃЌЉ2ЃЉЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌ
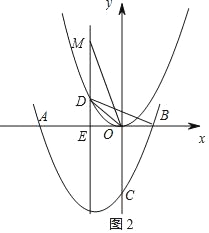
гЩ![]() ЕУ
ЕУ![]() ЃЌМДDЃЈЉ1ЃЌ1ЃЉЃЌ
ЃЌМДDЃЈЉ1ЃЌ1ЃЉЃЌ
дђDE=OD=1ЃЌ
ЁрЁїDOEЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯDOE=ЁЯODE=45ЁуЃЌЁЯBOD=135ЁуЃЌOD=![]() ЃЌ
ЃЌ
ЁпBO=1ЃЌ
ЁрBD=![]() ЃЌ
ЃЌ
ЁпЁЯBOD=135ЁуЃЌ
ЁрЕуMжЛФмдкЕуDЩЯЗНЃЌ
ЁпЁЯBOD=ЁЯODM=135ЁуЃЌ
ЁрЕБ![]() Лђ
Лђ![]() ЪБЃЌвдMЁЂOЁЂDЮЊЖЅЕуЕФШ§НЧаЮЁїBODЯрЫЦЃЌ
ЪБЃЌвдMЁЂOЁЂDЮЊЖЅЕуЕФШ§НЧаЮЁїBODЯрЫЦЃЌ
ЂйШє![]() ЃЌдђ
ЃЌдђ![]() ЃЌНтЕУDM=2ЃЌ
ЃЌНтЕУDM=2ЃЌ
ДЫЪБЕуMзјБъЮЊЃЈЉ1ЃЌ3ЃЉЃЛ
ЂкШє![]() ЃЌдђ
ЃЌдђ![]() ЃЌНтЕУDM=1ЃЌ
ЃЌНтЕУDM=1ЃЌ
ДЫЪБЕуMзјБъЮЊЃЈЉ1ЃЌ2ЃЉЃЛ
злЩЯЃЌЕуMзјБъЮЊЃЈЉ1ЃЌ3ЃЉЛђЃЈЉ1ЃЌ2ЃЉЃЎ