��Ŀ����
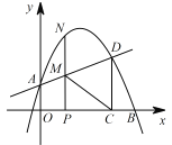
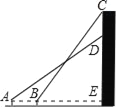
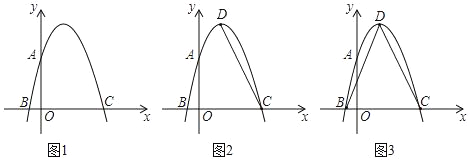
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������y=ax2+bx+3��x����B��C���㣨��B����C���ң�����y���ڵ�A����OA=OC��B����1��0����
��1����������ߵĽ���ʽ��
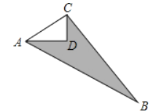
��2����ͼ2����DΪ�����ߵĶ��㣬����CD����P����������һ���㣬����C��D����֮���˶�������P��PE��y�ύ�߶�CD�ڵ�E�����P�ĺ�����Ϊt���߶�PE��Ϊd��д��d��t�Ĺ�ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
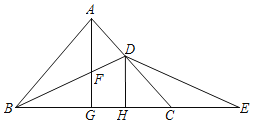
��3����ͼ3���ڣ�2���������£�����BD����BD����һ����Q����DQ=CE������EQ������BQE+��DEQ=90��ʱ�����ʱ��P�����꣮
���𰸡���1�������ߵĽ���ʽΪ��y=��x2+2x+3����2��d=��t2+4t��3����3��P��![]() ��
��![]() ����
����
��������
��1����������y=ax2+bx+3��y�ύ�ڵ�A������õ�A�����꣬��OA=OC������õ�C�����꣬Ȼ��ֱ����B,C���������a��b��������ö��κ����Ľ���ʽ��
��2�������ӳ�PE��x���ڵ�H���ֽ�����ʽ��Ϊ�������ʽ���D��1��4������ֱ��CD�Ľ���ʽΪy=kx+b���ٽ���C��3��0����D��1��4�����룬��y=��2x+6����E��t����2t+6����P��t����t2+2t+3����PH=��t2+2t+3��EH=��2t+6���ٸ���d=PH��EH���ɵô𰸣�
��3�����ȣ���DK��OC�ڵ�K����QM��x�ύDK�ڵ�T���ӳ�PE��EP��OC��H����QM��M����ER��DK�ڵ�R����QE��DK�Ľ���ΪN�����������ڣ�2������������֤����DQT�ա�ECH���ٸ���ȫ�������ε����ʼ��ɵ�ME=4��2����2t+6����QM= t��1+��3��t����������ô𰸣�
��1����x=0ʱ��y=3��
��A��0��3����OA=3��
��OA=OC��
��OC=3��
��C��3��0����
��������y=ax2+bx+3������B����1��0����C��3��0��
��![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪ��y=��x2+2x+3��
��2����ͼ1���ӳ�PE��x���ڵ�H��

��y=��x2+2x+3=����x��1��2+4��
��D��1��4����
��ֱ��CD�Ľ���ʽΪy=kx+b��
����C��3��0����D��1��4�����룬�ã�
![]() ��
��
��ã�![]() ��
��
��y=��2x+6��
��E��t����2t+6����P��t����t2+2t+3����
��PH=��t2+2t+3��EH=��2t+6��
��d=PH��EH=��t2+2t+3������2t+6��=��t2+4t��3��
��3����ͼ2����DK��OC�ڵ�K����QM��x�ύDK�ڵ�T���ӳ�PE��EP��OC��H����QM��M����ER��DK�ڵ�R����QE��DK�Ľ���ΪN��
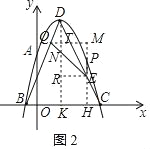
��D��1��4����B����1��0����C��3��0����
��BK=2��KC=2��
��DK��ֱƽ��BC��
��BD=CD��
���BDK=��CDK��
�ߡ�BQE=��QDE+��DEQ����BQE+��DEQ=90�㣬
���QDE+��DEQ+��DEQ=90������2��CDK+2��DEQ=90�㣬
���CDK+��DEQ=45��������RNE=45�㣬
��ER��DK��
���NER=45�㣬
���MEQ=��MQE=45�㣬
��QM=ME��
��DQ=CE����DTQ=��EHC����QDT=��CEH��
���DQT�ա�ECH��
��DT=EH��QT=CH��
��ME=4��2����2t+6����
QM=MT+QT=MT+CH=t��1+��3��t����
4��2����2t+6��=t��1+��3��t����
��ã�t=![]() ��
��
��P��![]() ��
��![]() ����
����

����Ŀ��ij�����û�����������![]() (��)���һ�ֲ�Ʒ������������
(��)���һ�ֲ�Ʒ������������![]() ��ÿ�����ۼ�Ϊ18��Ԫ��ÿ���ijɱ�
��ÿ�����ۼ�Ϊ18��Ԫ��ÿ���ijɱ�![]() (��Ԫ)�ǻ������븡���۵ĺͣ����л����۱��ֲ��䣬����������������
(��Ԫ)�ǻ������븡���۵ĺͣ����л����۱��ֲ��䣬����������������![]() (��)�ɷ��ȣ����г����з��֣���������
(��)�ɷ��ȣ����г����з��֣���������![]() ���·�
���·�![]() (
(![]() ������
Ϊ������![]() )���Ϲ�ϵʽ
)���Ϲ�ϵʽ![]() (
(![]() Ϊ����)���ҵõ��˱��е����ݣ�
Ϊ����)���ҵõ��˱��е����ݣ�
�·� | 1 | 2 |
�ɱ� | 11 | 12 |
������ | 120 | 100 |
(1)��![]() ��
��![]() ����Ĺ�ϵʽ����˵��һ����Ʒ�������ܷ���12��Ԫ��
����Ĺ�ϵʽ����˵��һ����Ʒ�������ܷ���12��Ԫ��
(2)��![]() �����ƶ��Ƿ����ij���¼���ӯ��Ҳ������
�����ƶ��Ƿ����ij���¼���ӯ��Ҳ������
(3)����һ��12�����У�����![]() ���º͵�
���º͵�![]() ���µ�������������
���µ�������������![]() ��
��