Question

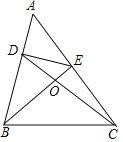
【题目】（1）如图，在△ABC中，∠A是锐角，点D，E分别在AB，AC上，且∠DCB＝∠EBC＝∠A，BE与CD相交于点O，探究BD与CE之间的数量关系，并证明你的结论．

（2）已知四边形ABCD，连接AC、BD交于O，且满足条件：AB+CD＝AD+BC，AB2+AD2＝BC2+DC2，请探究AC与BD的关系，并说明理由．

Answer 1

【答案】（1）BD＝CE，理由见解析；（2）AC与BD的关系是：BD垂直平分AC；理由见解析.

【解析】

（1）以C为顶点作∠FCB＝∠DBC，CF交BE于F点，证明△BDC≌△CFB（ASA），得出BD＝CF，∠BDC＝∠CFB，再证出∠CFB＝∠CEF，得出CE＝CF，即可得出结论；
（2）由AB＋DC＝AD＋BC，AB2＋AD2＝BC2＋DC2，可证得AB＝BC，DC＝AD，即可得出BD垂直平分AC．

解：（1）BD＝CE，

证明：以C为顶点作∠FCB＝∠DBC，CF交BE于F点，如图1所示：

在△BDC和△CFB中，，

∴△BDC≌△CFB（ASA），

∴BD＝CF，∠BDC＝∠CFB，

∵∠DCB＝∠EBC＝∠A，

∴∠DCB+∠EBC＝∠A，

∵∠DCB+∠EBC＝∠FOC，

∴∠FOC＝∠A，

∵∠BDC＝∠A+∠ACD，

∴∠CFB＝∠A+∠ACD，

∴∠CFB＝∠FOC+∠ACD，

∵∠FEC＝∠FOC+∠ACD，

∴∠CFB＝∠CEF，

∴CE＝CF，

∴BD＝CE；

（2）AC与BD的关系是：BD垂直平分AC；

理由：如图2所示：

∵AB2+AD2＝BC2+DC2，

∴AB2﹣DC2＝BC2﹣AD2，

∴（AB+DC）（AB﹣DC）＝（AD+BC）（BC﹣AD），

∵AB+DC＝AD+BC，

∴AB﹣DC＝BC﹣AD，

∴AB＝BC，DC＝AD，

∴点B在AC的垂直平分线上，点D在AC的垂直平分线上，

∴BD垂直平分AC．