题目内容
【题目】折叠圆心为
、半径为
的圆形纸片，使圆周上的某一点
与圆心重合．对圆周上的每一点，都这样折叠纸片，从而都有一条折痕．那么，所有折痕所在直线上点的全体为（ ）
A. 以为圆心、半径为的圆周 B. 以为圆心、半径为
的圆周
C. 以为圆心、半径为的圆内部分 D. 以为圆心、半径为的圆周及圆外部分
【答案】D
【解析】
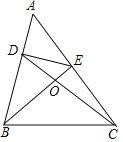
折叠圆心为O，半径为10cm的圆形纸片，圆周上的一点A与圆形O重合，此时折痕就是OA的垂直平分线，圆心O到折痕的最近距离是5cm，最远距离为10cm，对圆周上的每一个点都这样折叠，可以得到折痕上所有点形成的图形．
解：折叠圆心为O，半径为1cm的圆形纸片，当圆周上的点A与圆形O重合时，折痕就是OA的垂直平分线，圆心O到折痕的最近距离是5cm，最远距离是10cm，对圆周上的每一个点都这样折叠，所有折痕所在直线形成的图形应是一个圆环，圆环的圆心是O，小圆的半径是5cm，大圆的半径是10cm．
故选：D
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案【题目】甲乙两人在相同条件下完成了10次射击训练，两人的成绩如图所示。
根据以上信息，整理分析数据如下：
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
（1）完成表格；
（2）根据训练成绩，你认为选派哪一名队员参赛更好？为什么？
【题目】在一个不透明的盒子中装有颜色不同的8个小球，其中红球3个，黑球5个．
(1)先从袋中取出m(m＞1)个红球，再从袋中随机摸出1个球，将“摸出黑球”记为事件A.请完成下列表格：
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋中取出m个红球，再放入m个一样的黑球并摇匀，随机摸出1个球是黑球的概率是
，求m的值．
【题目】某中学举办“网络安全知识答题竞赛”，七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛，两个队各选出的5名选手的决赛成绩如图所示．
平均分（分） | 中位数（分） | 众数（分） | 方差（分2） | |
七年级 | a | 85 | b | S七年级2 |
八年级 | 85 | c | 100 | 160 |
（1）根据图示填空：a＝ ，b＝ ，c＝ ；
（2）结合两队成绩的平均数和中位数进行分析，哪个代表队的决赛成绩较好？
（3）计算七年级代表队决赛成绩的方差S七年级2，并判断哪一个代表队选手成绩较为稳定．
