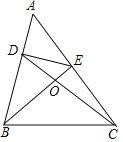
题目内容
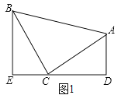
【题目】(1)(模型建立)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED与D,过B作BE⊥ED于E,求证:△BEC≌△CDA;
(2)(模型应用):已知直线![]() 与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;
与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;

【答案】(1)证明见解析;(2)y=![]() x+3
x+3
【解析】
(1)由条件可求得∠EBC=∠ACD,利用AAS可证明△BEC≌△CDA;(2)过C作CD⊥x轴于点D,由直线解析式可求得A、B的坐标,利用模型结论可得CD=BO,BD=AO,从而可求得C点坐标,利用待定系数法可求得直线AC的解析式
证明:(1)∵AD⊥ED, BE⊥ED
∴∠E=∠D=90°
又∵∠ACB=90°,
∴∠EBC+∠BCE=∠BCE+∠ACD=90°,
∴∠EBC=∠ACD,
在△BEC和△CDA中,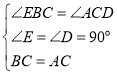
∴△BEC≌△CDA(AAS);
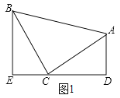
(2)如图,过C作CD⊥x轴于点D,
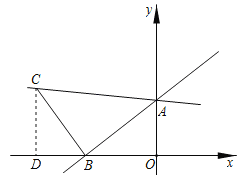
直线![]() 与y轴交于A点,与x轴交于B点,
与y轴交于A点,与x轴交于B点,
令y=0可求得x=-4,令x=0可求得y=3,
∴OA=3,OB=4,
同(1)可证得△CDB≌△BAO,
∴CD=BO=4,BD=AO=3,
∴OD=4+3=7,
∴C(-7,4),且A(0,3),
设直线AC解析式为y=kx+3,把C点坐标代入可得4=-7k+3,解得k=![]()
∴直线AC解析式为y=![]() x+3
x+3

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目