题目内容
【题目】如图，点A在x轴上，BC⊥y轴于C，点B的横坐标为a，AB＝2a，∠B＝120°，在y轴上找一点P，使PA+PB最小，请画出点P，并求PA+PB的最小值．
【答案】作图见解析；2
a．
【解析】
作点A关于y轴的对称点A′，再连接A′B，与y轴的交点即为所求，进而利用含30度角的直角三角形的性质和勾股定理解答即可．
解：作点A关于y轴的对称点A′，再连接A′B，与y轴的交点P即为所求，
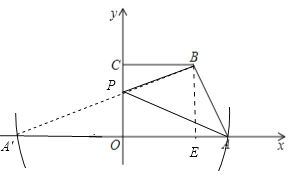
过点B作BE⊥x轴，
∵BC⊥y轴于C，点B的横坐标为a，AB＝2a，∠B＝120°，
∴BC∥x轴，∠BAE＝180°﹣∠ABC＝180°﹣120°＝60°，
∴AE＝a，OE＝a，BE＝a，
∴A'O＝OA＝OE+AE＝2a，
∴A'E＝2a+a＝3a，
∴A'B＝
．
∴PA+PB＝A'B＝2a．
练习册系列答案
阅读快车系列答案
相关题目
