题目内容
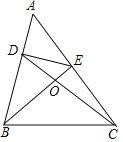
【题目】如图,BF和CE分别是钝角△ABC(∠ABC是钝角)中AC、AB边上的中线,又BF⊥CE,垂足是G,过点G作GH⊥BC,垂足为H.
(1)求证:GH2=BHCH;
(2)若BC=20,并且点G到BC的距离是6,则AB的长为多少?

【答案】(1)证明见解析(2)2![]()
【解析】
(1)只要证明△CGH∽△GBH即可解决问题;
(2)作EM⊥CB交CB的延长线于M.设CH=x,HB=y.构建方程组求出x、y,解直角三角形求出EM、BM即可.
(1)证明:∵CE⊥BF,GH⊥BC,
∴∠CGB=∠CHG=∠BHG=90°,
∴∠CGH+∠BGH=90°,∠BGH+∠GBH=90°,
∴∠CGH=∠GBH,
∴△CGH∽△GBH,
∴![]() ,
,
∴GH2=BHCH;
(2)解:作EM⊥CB交CB的延长线于M.设CH=x,HB=y.

则有![]() ,解得
,解得![]() 或
或![]() ,
,
∵∠ABC是钝角,
∴CH>BH,
∴CH=18,BH=2,
∵G是△ABC的重心,∴CG=2EG,
∵GH⊥BC,EM⊥BC,
∴GH∥EM,
∴![]() ,
,
∴EM=9,CM=27,
∴BM=CM﹣BC=7,
∴BE=![]() ,
,
∴AB=2BE=2![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?