题目内容
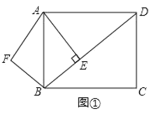
【题目】已知：如图①，在矩形ABCD中，AB＝5，
，AE⊥BD，垂足是E．点F是点E关于AB的对称点，连接AF、BF．
（1）求AE和BE的长；
（2）若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点F分别平移到线段AB、AD上时，求出相应的m的值；
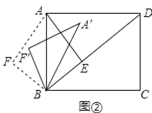
（3）如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的
为
，在旋转过程中，设
所在的直线与直线AD交于点P，与直线BD交于点Q，若△DPQ为等腰三角形，请直接写出此时DQ的长．
【答案】（1）4；3 （2）3或
（3）
或
【解析】
（1）由矩形的性质，利用勾股定理求解
的长，由等面积法求解
，由勾股定理求解
即可，
（2）利用对称与平移的性质得到：AB∥A′B′，∠4＝∠1，BF＝B′F′＝3．当点F′落在AB上时，证明BB′＝B′F′即可得到答案，当点F′落在AD上时，证明△B′F′D为等腰三角形，从而可得答案，
（3）分4种情况讨论：①如答图3﹣1所示，点Q落在BD延长线上，证明A′Q＝A′B，利用勾股定理求解
从而求解
，②如答图3﹣2所示，点Q落在BD上，证明点A′落在BC边上，利用勾股定理求解
从而可得答案，③如答图3﹣3所示，点Q落在BD上，证明∠A′QB＝∠A′BQ，利用勾股定理求解，从而可得答案，④如答图3﹣4所示，点Q落在BD上，证明BQ＝BA′，从而可得答案．
解：（1）在Rt△ABD中，AB＝5，
，
由勾股定理得：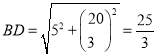
．
．
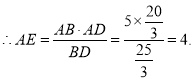
在Rt△ABE中，AB＝5，AE＝4，
由勾股定理得：BE＝3．
（2）设平移中的三角形为△A′B′F′，如答图2所示：
由对称的性质可知，∠1＝∠2．
由平移性质可知，AB∥A′B′，∠4＝∠1，BF＝B′F′＝3．
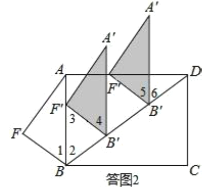
①当点F′落在AB上时，
∵AB∥A′B′，
∴∠3＝∠4，
∴∠3＝∠2，
∴BB′＝B′F′＝3，即m＝3；
②当点F′落在AD上时，
∵AB∥A′B′，∴∠6＝∠2，
∵∠1＝∠2，∠5＝∠1，∴∠5＝∠6，
A′B′⊥AD，
∴△B′F′D为等腰三角形，
∴B′D＝B′F′＝3，
，即
．
（3）DQ的长度分别为或．
在旋转过程中，等腰△DPQ依次有以下4种情形：
①如答图3﹣1所示，点Q落在BD延长线上，且PD＝DQ，
∠2＝2∠Q，
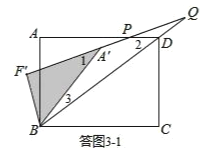
∵∠1＝∠3+∠Q，∠1＝∠2，
∴∠3＝∠Q，
∴A′Q＝A′B＝5，
∴F′Q＝F′A′+A′Q＝4+5＝9．
在Rt△BF′Q中，由勾股定理得：
．
；
②如答图3﹣2所示，点Q落在BD上，且PQ＝DQ，∴∠2＝∠P，
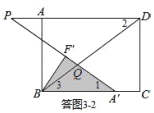
∵∠1＝∠2，∴∠1＝∠P，∴BA′∥PD，
∵PD∥BC，∴此时点A′落在BC边上．
∵∠3＝∠2，∴∠3＝∠1，
∴BQ＝A′Q，∴F′Q＝F′A′﹣A′Q＝4﹣BQ．
在Rt△BQF′中，由勾股定理得：
即：
解得：
，
；
③如答图3﹣3所示，点Q落在BD上，且PD＝DQ，
∠3＝∠4．
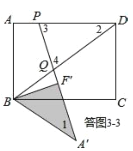
∵∠2+∠3+∠4＝180°，∠3＝∠4，
．
∵∠1＝∠2，
．
，
，
∴∠A′QB＝∠A′BQ，∴A′Q＝A′B＝5，
∴F′Q＝A′Q﹣A′F′＝5﹣4＝1．
在Rt△BF′Q中，由勾股定理得：
，
；
④如答图3﹣4所示，点Q落在BD上，且PQ＝PD，
∠2＝∠3．
∵∠1＝∠2，∠3＝∠4，∠2＝∠3，
∴∠1＝∠4，
∴BQ＝BA′＝5，
．
综上所述，DQ的长度分别为或．
