题目内容
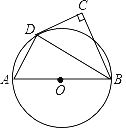
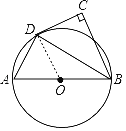
【题目】如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
(1)求证:CD是⊙O的切线;
(2)若∠CDB=60°,AB=18,求![]() 的长.
的长.
【答案】(1)见解析;(2)3π.
【解析】
(1)连接OD,求出OD//BC,求出OD⊥DC,根据切线的判定得出即可;
(2)求出∠CBD=30°,求出∠AOD=∠ABC=60°,求出半径OA,根据弧长公式求出即可.
(1)连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD平分∠ABC,
∴∠CBD=∠OBD,
∴∠CBD=∠ODB,
∴OD//BC,
∴∠C+∠ODC=180°,
∵∠C=90°.
∴∠ODC=90°,即OD⊥DC,
∵OD过O,
∴CD是⊙O的切线;
(2)∵∠CDB=60°,∠C=90°,
∴∠CBD=30°,
∵BD平分∠ABC,
∴∠ABC=60°,
∵OD//BC,
∴∠AOD=∠ABC=60°,
∵直径AB=18,
∴半径OA=9,
∴弧AD的长是![]() =3π.
=3π.

练习册系列答案
相关题目
【题目】某中学号召全校学生进行安全教育网络学习,并对部分学生的学习情况进行了随机调查.对部分学生的成绩(x为整数,满分100分)进行统计,并绘制了如下统计图表.
调查结果频数分布表
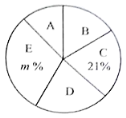
| 调查结果扇形统计图
|
根据所给信息,解答下列问题:
(1)填空:![]() _________,
_________,![]() _________;
_________;
(2)求扇形统计图中,m的值及A组对应的圆心角的度数;
(3)若参加学习的同学共有1500人,请你估计成绩不低于80分的同学有多少人.