��Ŀ����
����Ŀ��ij�羰���ڵĹ�·��ͼ1��ʾ������������ѵİ������ڴ������ظù�·�����ݵ飬;��ͣ�����֣����³�ʱ����Բ��ƣ�����һ�����8�㷢�����Ժ�ÿ��10������һ�����ڴ�������С����ĩ���÷羰�����棬����7��40������ڴ�����û�������ʱ�䣬���ǴӾ�����ڴ��������ظù�·����25���Ӻ����֣�����ڴ���·��y���ף���ʱ��x���֣��ĺ�����ϵ��ͼ2��ʾ��
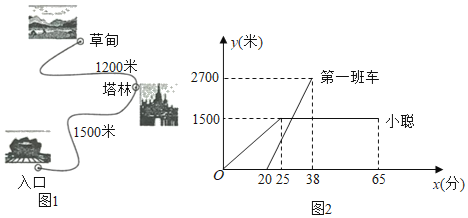
��1�����һ�����ڴ���·��y���ף���ʱ��x���֣���������ʽ����д��x��ȡֵ��Χ��
��2�����һ�����ڴ��������������ʱ�䣻
��3��С������������40���Ӻ���������ݵ飬��С�������ܹ����ϵڼ����������������ݵ飬��������������������������е��ݵ������˼����ӣ�������ÿһ��ٶȾ���ͬ��С�ϲ����ٶȲ��䣩
���𰸡���1��y��150x��3000��20��x��38������2����һ�����ڴ�������������ʱ��10���ӣ���3����������������������������е��ݵ�������7���ӣ�
��������
��1����y��kx+b�����ô���ϵ������⼴�ɣ�
��2����y��1500���루1���Ľ��ۼ��ɣ�
��3����С�������˵�n���30��25+10(n��1)��40�����n��4.5���ɵ�С�������˵�5����ٸ�����·�̡��ٶ���ʱ��Ĺ�ϵ����ɣ�
��1��������ã����躯������ʽΪ��y��kx+b(k��0)��
��(20��0)��(38��2700)����y��kx+b��
��![]() ��
��
���![]() ��
��
����һ�����ڴ���·��y(��)��ʱ��x(��)�ĺ�������Ϊy��150x��3000(20��x��38)��
��2����y��1500����y��150x��3000�����x��30��
30��20��10(��)��
����һ�����ڴ�������������ʱ��10���ӣ�
��3����С�������˵�n�����
30��25+10(n��1)��40�����n��4.5��
��С�������˵�5���
�ȳ���ʱ��Ϊ5���ӣ��������ʱ��Ϊ��1200��150��8(��)��
��������ʱ�䣺1200��(1500��25)��20(��)��
20��(8+5)��7(��)��
����������������������������е��ݵ�������7���ӣ�

 ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�