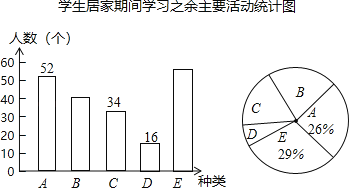
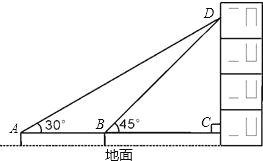
题目内容
【题目】已知:△ABC内接于⊙O,连接CO并延长交AB于点E,交⊙O于点D,满足∠BEC=3∠ACD.

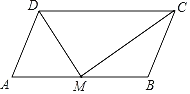
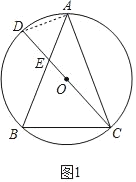
(1)如图1,求证:AB=AC;
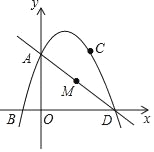
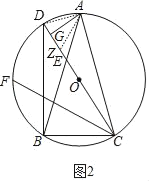
(2)如图2,连接BD,点F为弧BD上一点,连接CF,弧CF=弧BD,过点A作AG⊥CD,垂足为点G,求证:CF+DG=CG;
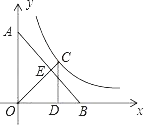
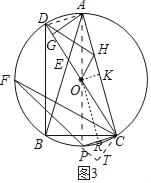
(3)如图3,在(2)的条件下,点H为AC上一点,分别连接DH,OH,OH⊥DH,过点C作CP⊥AC,交⊙O于点P,OH:CP=1:![]() ,CF=12,连接PF,求PF的长.
,CF=12,连接PF,求PF的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接AD.设∠BEC=3α,∠ACD=α,利用等量代换得出∠ABC=∠ACB,最后进一步证明结论即可;
(2)连接AD,在CD上取一点Z,使得CZ=BD,通过证明△ADB≌△AZC得出AD=AZ,然后进一步证明即可;
(3)连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T,利用三角函数以及勾股定理进一步求解即可.
(1)证明:如图1中,连接AD.设∠BEC=3α,∠ACD=α.
∵∠BEC=∠BAC+∠ACD,
∴∠BAC=2α,
∵CD是直径,
∴∠DAC=90°,
∴∠D=90°﹣α,
∴∠B=∠D=90°﹣α,
∵∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣2α﹣(90°﹣α)=90°﹣α.
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:如图2中,连接AD,在CD上取一点Z,使得CZ=BD.
∵弧BD=弧CF,
∴DB=CF,
∵∠DBA=∠DCA,CZ=BD,AB=AC,
∴△ADB≌△AZC(SAS),
∴AD=AZ,
∵AG⊥DZ,
∴DG=GZ,
∴CG=CZ+GZ=BD+DG=CF+DG.
(3)连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T.
∵CP⊥AC,
∴∠ACP=90°,
∴PA是直径,
∵OR⊥PC,OK⊥AC,
∴PR=RC,∠ORC=∠OKC=∠ACP=90°,
∴四边形OKCR是矩形,
∴RC=OK,
∵OH:PC=1:![]() ,
,
∴设OH=![]() a,PC=2a,
a,PC=2a,
∴PR=RC=a,
∴RC=OK=a,sin∠OHK=![]() ,
,
∴∠OHK=45°,
∵OH⊥DH,
∴∠DHO=90°,
∴∠DHA=180°﹣90°﹣45°=45°,
∵CD是直径,
∴∠DAC=90°,
∴∠ADH=90°﹣45°=45°,
∴∠DHA=∠ADH,
∴AD=AH,
∵∠COP=∠AOD,
∴AD=PC,
∴AH=AD=PC=2a,
∴AK=AH+HK=2a+a=3a,
在Rt△AOK中,tan∠OAK=![]() ,OA=
,OA=![]() =
=![]() ,
,
∴sin∠OAK=![]() ,
,
∵∠ADG+∠DAG=90°,∠ACD+∠ADG=90°,
∴∠DAG=∠ACD,
∵AO=CO,
∴∠OAK=∠ACO,
∴∠DAG=∠ACO=∠OAK,
∴tan∠ACD=tan∠DAG=tan∠OAK=![]() ,
,
∴AG=3DG,CG=3AG,
∴CG=9DG,
由(2)可知,CG=DG+CF,
∴DG+12=9DG,
∴DG=![]() ,AG=3DG=3×
,AG=3DG=3×![]() =
=![]() ,
,
∴AD=![]() ,
,
∴PC=AD=![]() ,
,
∵sin∠F=sin∠OAK,
∴sin∠F=![]() ,
,
∴CT=![]() =
=![]() ×12=
×12=![]() ,FT=
,FT=![]() ,PT=
,PT=![]() ,
,
∴PF=FT﹣PT=![]() ﹣
﹣![]() =
=![]() .
.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案