题目内容
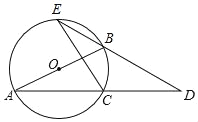
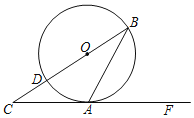
【题目】如图,在![]() 中,
中,![]() .半径为
.半径为![]() 的圆
的圆![]() 与边
与边![]() 相交于点
相交于点![]() 与边
与边![]() 相交于点
相交于点![]() 连结
连结![]() 并延长,与线段
并延长,与线段![]() 的延长线交于点
的延长线交于点![]() .
.
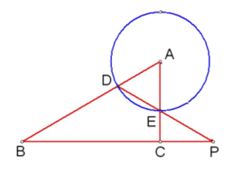
(1)当![]() 时,连结
时,连结![]() 若
若![]() 与
与![]() 相似,求
相似,求![]() 的长;
的长;
(2)若![]() 求
求![]() 的正切值;
的正切值;
(3)若![]() ,设
,设![]() 的周长为
的周长为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,其中
,其中![]()
【解析】
(1)当∠B=30°时,∠A=60°,此时△ADE是等边三角形,则∠PEC=∠AED=60°,由此可证得∠P=∠B=30°;若△AEP与△BDP相似,那么∠EAP=∠EPA=∠B=∠P=30°,此时EP=EA=1,即可在Rt△PEC中求得CE的长;
(2)若BD=BC,可在Rt△ABC中,由勾股定理求得BD、BC的长;过C作CF∥DP交AB于F,易证得△ADE∽△AFC,根据得到的比例线段可求出DF的长;进而可通过证△BCF∽△BPD,根据相似三角形的对应边成比例求得BP、BC的比例关系,进而求出BP、CP的长;在Rt△CEP中,根据求得的CP的长及已知的CE的长即可得到∠BPD的正切值;
(3)过点D作DQ⊥AC于Q,可用未知数表示出QE的长,根据∠BPD(即∠EDQ)的正切值即可求出DQ的长;在Rt△ADQ中,可用QE表示出AQ的长,由勾股定理即可求得EQ、DQ、AQ的长;易证得△ADQ∽△ABC,根据得到的比例线段可求出BD、BC的表达式,进而可根据三角形周长的计算方法得到y、x的函数关系式.
![]() 解:
解:![]()
![]()
![]()
![]()
![]()
![]() 三角形
三角形![]() 为等腰三角形
为等腰三角形
![]() 与
与![]() 相似
相似
![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]() 过点
过点![]() 作
作![]() 于点
于点![]() ,
,
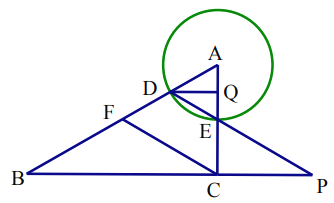
且设![]()
![]()
![]()
![]()
![]() 与
与![]() 相似
相似
![]()
即![]()
![]()
在![]() 中,
中,
![]()
![]()
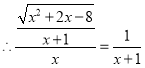
解之得![]() ,
,
即![]()
过点![]() 作
作![]()
![]() 与
与![]() 相似,
相似,
![]() ,
,
即![]() ,
,
即![]()
![]()
![]() 与
与![]() 相似
相似
![]() ,
,
即:![]()
![]()
![]() 过点
过点![]() 作
作![]() 于点
于点![]() ,
,
则![]() 与
与![]() 相似,
相似,
设![]() ,则
,则![]()
![]() 且
且![]()
![]()
![]() 在
在![]() 中,
中,
据勾股定理得:![]()
即:![]() ,
,
解之得![]() (舍去)
(舍去)![]()
![]() 与
与![]() 相似
相似
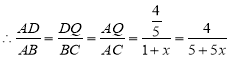
![]()
![]() 三角形
三角形![]() 的周长
的周长![]()
即:![]() ,其中
,其中![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目