题目内容
【题目】已知∠BAE与∠BCD互为补角，AB＝AE，CB＝CD，连接ED，点P为ED的中点．
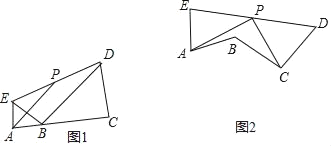
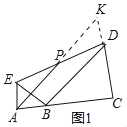
（1）如图1，若点A，B，C三点在同一条直线上．
①求证：∠EBD＝90°；②求证：AP∥BD；
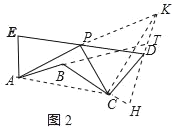
（2）如图2，若点A，B，C三点不在同一条直线上，求证：AP⊥CP．
【答案】（1）①见解析；②见解析；（2）见解析.
【解析】
（1）①设∠EAB=x，∠BCD=y，由∠BAE与∠BCD互为补角，得出x+y=180°，AE∥CD，由AE=AB，得出∠ABE=90°-
x，由CB=CD，得出∠CBD=90°-y，即可得出结论；
②延长AP交CD延长线于点K，由AE∥CD，得出∠EAP=∠DKP，由AAS证得△AEP≌△KDP，得出DK=AE=AB，证得CA=CK，得出∠CAP=90°-y=∠CBD，即可得出结论；
（2）设∠EAB=x，∠BCD=y，延长AP到K，使PK=AP，连接KD，由SAS证得△AEP≌△KDP，得出KD=AE，∠EAP=∠DKP，AE∥KD，延长AB交KD于点T，延长KD交BC延长线于点H，则∠ATK=180°-∠EAB=180°-x=y，证得∠ATK=∠BCD=y，∠DCH=∠BTH，得出∠TBC=∠CDH，∠ABC=∠KDC，连接AC、KC，由SAS证得△ABC≌△KDC（SAS），得出CA=CK，即可得出结论．
（1）①设∠EAB＝x，∠BCD＝y，
∵∠BAE与∠BCD互为补角，
∴x+y＝180°，AE∥CD，
∵AE＝AB，
∴∠ABE＝90°﹣x，
∵CB＝CD，
∴∠CBD＝90°﹣y，
∴∠EBD＝180°﹣∠ABE﹣∠CBD＝180°﹣90°+x﹣90°+y＝（x+y）＝90°；
②延长AP交CD延长线于点K，如图1所示：
∵AE∥CD，
∴∠EAP＝∠DKP，
在△AEP和△KDP中，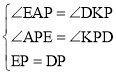 
∴△AEP≌△KDP（AAS），
∴DK＝AE＝AB，
∵CB＝CD，
∴CA＝CK，
∴∠CAP＝90°﹣y＝∠CBD，
∴AP∥BD；
（2）设∠EAB＝x，∠BCD＝y，
∵∠BAE与∠BCD互为补角，
∴x+y＝180°，
延长AP到K，使PK＝AP，连接KD，如图2所示：
在△AEP和△KDP中，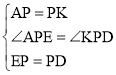
∴△AEP≌△KDP（SAS），
∴KD＝AE，∠EAP＝∠DKP，
∴AE∥KD，
延长AB交KD于点T，延长KD交BC延长线于点H，则∠ATK＝180°﹣∠EAB＝180°﹣x＝y，
∴∠ATK＝∠BCD＝y，
∴∠DCH＝∠BTH，
∵∠H＝∠H，
∴∠TBC＝∠CDH，
∴∠ABC＝∠KDC，
连接AC、KC，
在△ABC和△KDC中，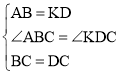 
∴△ABC≌△KDC（SAS），
∴CA＝CK，
∵PA＝PK，
∴AP⊥CP．
