题目内容
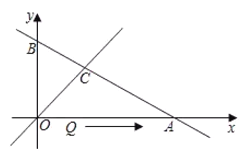
【题目】如图,直线![]() 与坐标轴分别交于点
与坐标轴分别交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的长为___________.
的长为___________.
【答案】2或![]() 或4
或4
【解析】
先求出直线![]() 与直线
与直线![]() 交点C的坐标,若使
交点C的坐标,若使![]() 是等腰三角形,分三种情况讨论,即OQ=CQ或OC=OQ或OC=CQ,在直角三角形中利用勾股定理,根据等腰三角形的性质即可求出OQ.
是等腰三角形,分三种情况讨论,即OQ=CQ或OC=OQ或OC=CQ,在直角三角形中利用勾股定理,根据等腰三角形的性质即可求出OQ.
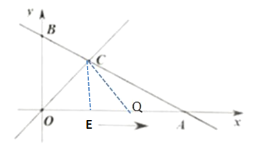
①如图,当OQ=CQ时,过点C作CE⊥OA于点E,
直线![]() 与直线
与直线![]() 交于点C,
交于点C,
![]()
得x=2,
y=x=2
∴C(2,2)
设OQ=CQ=x,QE=2-x
在Rt△CEQ中![]()
解得x=2
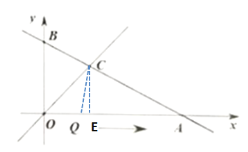
②当OC=OQ时,过点C作CE⊥OA于点E,C(2,2)
在Rt△CEO中, ![]()
OC=![]()
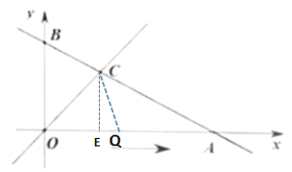
③当OC=CQ时, 过点C作CE⊥OA于点E
∵OC=CQ
∴OE=EQ=2
∴OQ=2OE=4
综上所示,若![]() 是等腰三角形,OQ的长为2或
是等腰三角形,OQ的长为2或![]() 或4
或4
故答案为:2或![]() 或4
或4

练习册系列答案
相关题目