题目内容
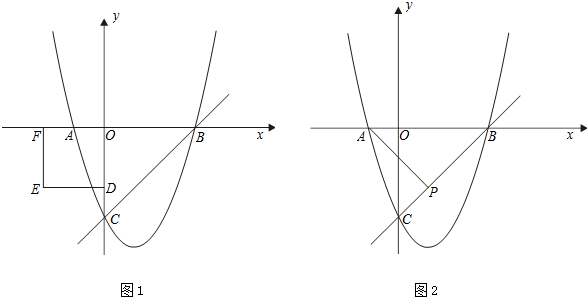
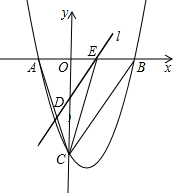
如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物 线的顶点,且A,C两点的横坐标分别为1和4.
线的顶点,且A,C两点的横坐标分别为1和4.
(1)求A,B两点的坐标;
(2)求二次函数的函数表达式;
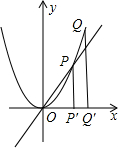
(3)在(2)的抛物线上,是否存在点P,使得∠BAP=45°?若存在,求出点P的坐标及此时△ABP的面积;若不存在,请说明理由.
 线的顶点,且A,C两点的横坐标分别为1和4.
线的顶点,且A,C两点的横坐标分别为1和4.(1)求A,B两点的坐标;
(2)求二次函数的函数表达式;
(3)在(2)的抛物线上,是否存在点P,使得∠BAP=45°?若存在,求出点P的坐标及此时△ABP的面积;若不存在,请说明理由.
(1)因为A,C两点的横坐标分别为1,4,
所以点A(1,0).(1分)
又点A,B关于对称轴x=4对称,点B(7,0).(2分)
(2)因为二次函数y=ax2+bx-7的图象经过点A(1,0),B(7,0).
所以
(4分)
解得:
(6分).
所以二次函数的表达式为y=-x2+8x-7.(7分)
(3)假设抛物线上存在点P(x,y),使得∠BAP=45°(8分)
①当点P在x轴上方时有x-1=y,
∴x-1=-x2+8x-7,
即x2-7x+6=0.
解得:x=6或x=1(不合题意舍去)
∴y=-62+8×6-7=5.
∴点P为(6,5).(9分)
此时,S△ABP=
×(7-1)×5=
=15(10分).
②当点P在x轴的下方时,有x-1=-y.
∴x-1=x2-8x+7,
解得:x=8或x=1(不合题意舍去)
∴y=-82+8×8-7=-7.
∴点P为(8,-7).(11分)
此时,S△ABP=
×(7-1)×7=
=21(12分).
所以点A(1,0).(1分)
又点A,B关于对称轴x=4对称,点B(7,0).(2分)
(2)因为二次函数y=ax2+bx-7的图象经过点A(1,0),B(7,0).
所以
|
解得:
|
所以二次函数的表达式为y=-x2+8x-7.(7分)
(3)假设抛物线上存在点P(x,y),使得∠BAP=45°(8分)
①当点P在x轴上方时有x-1=y,
∴x-1=-x2+8x-7,
即x2-7x+6=0.
解得:x=6或x=1(不合题意舍去)
∴y=-62+8×6-7=5.
∴点P为(6,5).(9分)
此时,S△ABP=
| 1 |
| 2 |
| 30 |
| 2 |
②当点P在x轴的下方时,有x-1=-y.
∴x-1=x2-8x+7,
解得:x=8或x=1(不合题意舍去)
∴y=-82+8×8-7=-7.
∴点P为(8,-7).(11分)
此时,S△ABP=
| 1 |
| 2 |
| 42 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
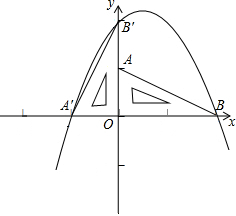 将此三角板绕原点O逆时针旋转90°,得到△A′B′O.
将此三角板绕原点O逆时针旋转90°,得到△A′B′O.