题目内容
如图甲,分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为x轴、y轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在x轴上),抛物线y=
x2+bx+c经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
(1)求B点坐标;
(2)求证:ME是⊙P的切线;
(3)设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,
①求△ACQ周长的最小值;
②若FQ=t,S△ACQ=S,直接写出S与t之间的函数关系式.

| 1 |
| 4 |
(1)求B点坐标;
(2)求证:ME是⊙P的切线;
(3)设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,
①求△ACQ周长的最小值;
②若FQ=t,S△ACQ=S,直接写出S与t之间的函数关系式.

(1)如图甲,连接PE、PB,设PC=n,
∵正方形CDEF的面积为1,
∴CD=CF=1,
根据圆和正方形的轴对称性知:OP=PC=n,
∴BC=2PC=2n,
∵而PB=PE,
∴PB2=BC2+PC2=4n2+n2=5n2,PE2=PF2+EF2=(n+1)2+1,
∴5n2=(n+1)2+1,
解得:n=1或n=-
(舍去),
∴BC=OC=2,
∴B点坐标为(2,2);
(2)证明:如图甲,由(1)知A(0,2),C(2,0),
∵A,C在抛物线上,
∴
,
解得:
,
∴抛物线的解析式为:y=
x2-
x+2=
(x-3)2-
,
∴抛物线的对称轴为x=3,即EF所在直线,
∵C与G关于直线x=3对称,
∴CF=FG=1,
∴MF=
FG=
,
在Rt△PEF与Rt△EMF中,
∠EFM=∠EFP,
∵
=
=
,
=
,
∴
=
,
∴△PEF∽△EMF,
∴∠EPF=∠FEM,
∴∠PEM=∠PEF+∠FEM=∠PEF+∠EPF=90°,
∴ME是⊙P的切线;
(3)①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=3于Q,连AQ,
则有AQ=A′Q,
∴△ACQ周长的最小值为AC+A′C的长,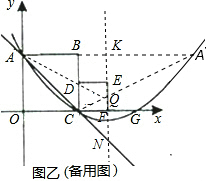
∵A与A′关于直线x=3对称,
∴A(0,2),A′(6,2),
∴A′C=
=2
,而AC=
=2
,
∴△ACQ周长的最小值为2
+2
;
②当Q点在F点上方时,S=S梯形ACFK-S△AKQ-S△CFQ=
×(3+1)×2-
×(2-t)×3-
×t×1=t+1,
同理,可得:当Q点在线段FN上时,S=1-t,
当Q点在N点下方时,S=t-1.

∵正方形CDEF的面积为1,
∴CD=CF=1,
根据圆和正方形的轴对称性知:OP=PC=n,
∴BC=2PC=2n,
∵而PB=PE,
∴PB2=BC2+PC2=4n2+n2=5n2,PE2=PF2+EF2=(n+1)2+1,
∴5n2=(n+1)2+1,
解得:n=1或n=-
| 1 |
| 2 |
∴BC=OC=2,
∴B点坐标为(2,2);
(2)证明:如图甲,由(1)知A(0,2),C(2,0),
∵A,C在抛物线上,
∴
|
解得:
|
∴抛物线的解析式为:y=
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴抛物线的对称轴为x=3,即EF所在直线,
∵C与G关于直线x=3对称,
∴CF=FG=1,
∴MF=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△PEF与Rt△EMF中,
∠EFM=∠EFP,
∵
| FM |
| EF |
| ||
| 1 |
| 1 |
| 2 |
| EF |
| PF |
| 1 |
| 2 |
∴
| FM |
| EF |
| EF |
| PF |
∴△PEF∽△EMF,
∴∠EPF=∠FEM,
∴∠PEM=∠PEF+∠FEM=∠PEF+∠EPF=90°,
∴ME是⊙P的切线;
(3)①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=3于Q,连AQ,
则有AQ=A′Q,
∴△ACQ周长的最小值为AC+A′C的长,

∵A与A′关于直线x=3对称,
∴A(0,2),A′(6,2),
∴A′C=
| (6-2)2+22 |
| 5 |
| 22+22 |
| 2 |
∴△ACQ周长的最小值为2
| 2 |
| 5 |
②当Q点在F点上方时,S=S梯形ACFK-S△AKQ-S△CFQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
同理,可得:当Q点在线段FN上时,S=1-t,
当Q点在N点下方时,S=t-1.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目




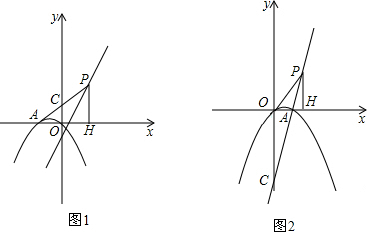
 线的顶点,且A,C两点的横坐标分别为1和4.
线的顶点,且A,C两点的横坐标分别为1和4.