题目内容
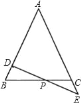
【题目】如图所示,在△ABC中,AB=AC,D为AB上一点,E为AC延长线上的一点,且CE=BD,连接DE交BC于点P.
(1)求证:PE=PD;
(2)若CE:AC=1:5,BC=10,求BP的长.
【答案】(1)见解析;(2)6.
【解析】
(1)过点D作DF∥AC交BC于点F,根据平行线的性质可得:∠ACB=∠DFB,∠FDP=∠E,根据AB=AC,可得∠ACB=∠ABC,进而可得∠ABC=∠DFB,因此DF=DB,再根据CE=BD,可得CE=DF,根据∠DPF=∠CPE,利用全等三角形的判定定理可得:△ECP≌△DFP,根据全等三角形性质可得PE=PD,
(2)根据CE=BD,AC=AB,CE:AC=1:5,可得BD:AB=1:5,
根据DF∥AC,可证得△BDF∽△BAC,根据相似三角形的性质可得![]() ,
,
由BC=10,代入上式可得BF=2,FC=8,根据△DFP≌△ECP,可得FP=PC,因此PF=4,继而可得BP=BF+FP=6.
(1)证明:过点D作DF∥AC交BC于点F,
∴∠ACB=∠DFB,∠FDP=∠E,
∵AB=AC(已知),
∴∠ACB=∠ABC,
∴∠ABC=∠DFB,
∴DF=DB,
又∵CE=BD(已知),
∴CE=DF,
又∵∠DPF=∠CPE,
∴△ECP≌△DFP,
∴PE=PD,
(2)解:∵CE=BD,AC=AB,CE:AC=1:5(已知),
∴BD:AB=1:5,
∵DF∥AC,
∴△BDF∽△BAC,
∴![]() ,
,
∵BC=10,
∴BF=2,FC=8,
∵△DFP≌△ECP,
∴FP=PC,
∴PF=4,
则BP=BF+FP=6.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目