题目内容
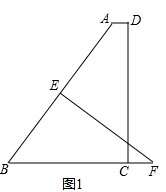
【题目】如图,将矩形ABCD沿MN折叠,使点B与点D重合. 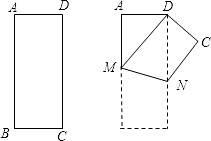
(1)求证:DM=DN;
(2)当AB和AD满足什么数量关系时,△DMN是等边三角形?并说明你的理由.
【答案】
(1)证明:由题意知∠1=∠2,
又AB∥CD,得∠1=∠3,
则∠2=∠3.
故DM=DN
(2)解:当AB= ![]() AD时,△DMN是等边三角形.
AD时,△DMN是等边三角形.
证明:连接BD.
∵∠A=90°,AB= ![]() AD,
AD,
∴tan∠ABD= ![]() =
= ![]() ,
,
∴∠ABD=30°.
∵BM=MD,
∴∠ABD=∠MDB=30°,
∴∠BMD=120°.
∴∠1=∠2=60°.
又DM=DN,
∴△DMN是等边三角形.
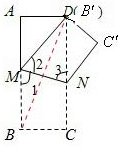
【解析】(1)根据矩形对边平行得∠1=∠3,根据折叠的性质得∠1=∠2,所以∠2=∠3,得DM=DN;(2)假设△DMN是等边三角形,则∠ADM=30°.有MD=2AM,AD= ![]() AM,AB=3AM,得AB=
AM,AB=3AM,得AB= ![]() AD.
AD.
【考点精析】关于本题考查的等边三角形的判定和翻折变换(折叠问题),需要了解三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】某中学在安全工作月中,进行了“防自然灾害﹣地震知识知多少”专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,花粉等级后的数据整理如下表:
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 40 | 120 | n | 4 |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m的值为 , n的值为;
(2)根据表中的数据,请你计算“非常了解”的频率在如图中对应的扇形的圆心角的度数,并补全扇形统计图; 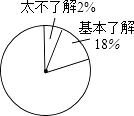
(3)若校一共有2400名学生,请根据调查结果估计全校学生中“比较了解”的人数为多少?
【题目】温度的度量有两种基本单位:摄氏温度(℃),华氏温度(℉).在温度计上,摄氏温度x与华氏温度y有如下表所示的对应关系:
x/℃ | … | -10 | 0 | 10 | 20 | … |
y/℉ | … | 14 | 32 | 50 | 68 | … |
按下列步骤确定y与x之间的函数关系式.
(1)在平面直角坐标系中描点、连线,画出图象;
(2)猜想能表示y与x之间关系的函数类型;
(3)确定y与x之间的函数关系式,并验证你的想法.