题目内容
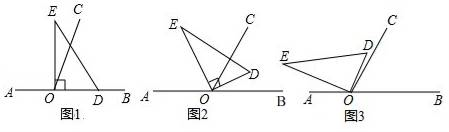
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

【答案】(1)30;(2)答案见解析;(3)65°或52.5°.
【解析】试题分析:(1)根据图形得出∠COE=∠BOE-∠COB,代入求出即可;
(2)根据角平分线定义求出∠COE=∠AOE=![]() ∠COA,再根据∠AOE+∠DOB=90°,∠COE+∠COD=90°,可得∠COD=∠DOB,从而问题得证;
∠COA,再根据∠AOE+∠DOB=90°,∠COE+∠COD=90°,可得∠COD=∠DOB,从而问题得证;
(3)设∠COD=x°,则∠AOE=5x°,根据题意则可得6x=30或5x+90﹣x=120,解方程即可得.
试题解析:(1)∵∠BOE=∠COE+∠COB=90°,
又∵∠COB=60°,
∴∠COE=∠BOE-∠COB=30°,
故答案为:30;
(2)∵OE平分∠AOC,
∴∠COE=∠AOE=![]() ∠COA,
∠COA,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,
∴∠COD=∠DOB,
∴OD所在射线是∠BOC的平分线;
(3)设∠COD=x°,则∠AOE=5x°,
∵∠DOE=90°,∠BOC=60°,
∴6x=30或5x+90﹣x=120,
∴x=5或7.5,
即∠COD=65°或37.5°,
∴∠BOD=65°或52.5°.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
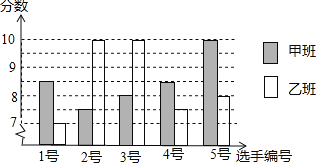
![]() 根据上图填写下表:
根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
| ______ | ______ |
乙班 |
| ______ | 10 |
|
![]() 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.