题目内容
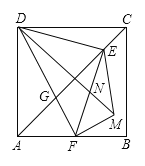
【题目】如图,△ABC中,AC=BC=4,∠ACB=90°,D为边AB上一动点(不与A、B重合),⊙D与BC切于E点,E点关于CD的对称点F在△ABC的一边上,则BD=______.
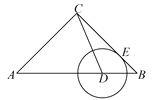
【答案】![]() 或
或![]() ;
;
【解析】
分为当E点关于CD的对称点F在AB或者AC上进行讨论:
①当F在AB边上时,根据对称性得出CE=CF,DE=DF,作![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,在直角三角形CHF中,用勾股定理解出
,在直角三角形CHF中,用勾股定理解出![]() 即可得出答案;
即可得出答案;
②当F在AC边上时,根据对称性知圆与AC、BC均相切,此时D在AB的中点,从而求解.
解:①当F在AB边上时,作![]() ,连接DF、CF,如图:
,连接DF、CF,如图:
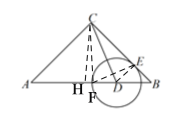
根据对称性知:CE=CF,DE=DF
又∵AC=BC=4,∠ACB=90°
∴![]() ,△DEB是等腰直角三角形
,△DEB是等腰直角三角形
设![]() ,则
,则![]() ,
,![]()
∴![]()
在直角三角形CHF中:![]()
即:![]() 解得:
解得:![]()
∴![]()
②当F在AC边上时,根据对称性知圆与AC、BC均相切,此时此时D在AB的中点,如图:
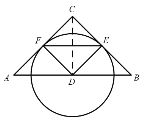
∴![]()
故答案为:![]() 或
或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目