题目内容
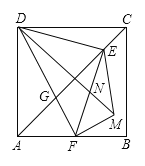
【题目】如图，正方形
中，
，点
是对角线
上一点，连接
，过点作
，交
于点
，连接
，交于点
，将
沿
翻折，得到
，连接
，交于点
，若点是的中点，则
的周长是（ ）
A.
B.
C.
D.
【答案】C
【解析】
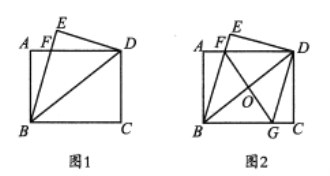
如图：过E作PQ⊥DC，交DC于P，交AB于Q，连接BE．先通过等腰三角形和全等三角形的判定和性质得到FQ=BQ=PE=1；再说明△DEF是等腰直角三角形，然后再利用勾股定理计算得到DE=EF=
；如图2，由DC//AB可得△DGC∽△FGA，列比例式可求FG和CG的长，从而得EG的长；然后再根据AGHF是等腰直角三角形，求得GH和FH的长；利用DE∥GM证明△DEN∽△MNH，则
可得EN=
，然后计算出△EMN各边的长，最后求周长即可．
解：如图1：过E作PQ⊥DC，交DC于P，交AB于Q，连接BE．
∵DC∥AB
∴PQ⊥AB，
∴四边形ABCD是正方形
∴∠ACD=450
∴△PEC是等腰直角三角形
∴PE=PC.
设PC=x，则PE=x，PD=4-x，EQ=4-x.
∴PD=EQ，
∴∠DPE=∠EQF=90°，∠PED=∠EFQ.
∴△DPE≌△EQF
∴DE=EF
∵DE⊥EF
∴△DEF是等腰直角三角形
易证△DEC≌△BEC
∴DE=BE
∴EF=BE
∵EQ⊥FB
∴FQ=BQ=
BF
∵AB=4，F是AB的中点
∴BF=2
∴FQ=BQ=PE=1
∴CE=
，PD=4-1=3
Rt△DAF中，
∴DE=EF=
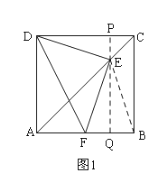
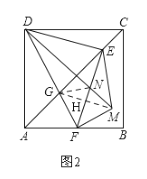
如图2：∵DC//AB.
∴△DGC∽△FGA
∴
∴AG=2AG,DG=2FG
∴
∵
∴
∴
连接GM、GN，交EF于H.
∵∠GFE=45°
∴△GHF是等腰直角三角形
∴
由折叠得：GM⊥EF，MH=GH=
∴∠EHM=∠DEF=90°
∴DE∥HM
∴△DEN∽△MNH
∴
∴
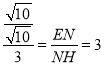
∴EN=3NH
∵EN+NH=EH=
∴EN=
∴NH=EH-EN=
在Rt△GNH中，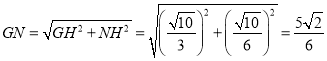
由折叠得：MN=GN，EM=EG
∴△EMN的周长为
．
故选：C．
