题目内容
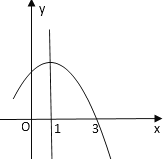
【题目】在平面直角坐标系中，抛物线
与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点B的坐标为（3,0），将直线
沿y轴向上平移3个单位长度后恰好经过B、C两点．
（1）求直线BC及抛物线的解析式；
（2）设抛物线的顶点为D，点P在抛物线的对称轴上，且
，求点P的坐标；
（3）连结CD，求∠OCA与∠OCD两角和的度数．
【答案】（1）y=－x+3；y=
－4x+3；（2）（2,2）或（2，－2）；（3）45°
【解析】
（1）根据平移得出点C的坐标，然后设出函数解析式，利用待定系数法求出函数解析式；
（2）根据二次函数得出点D和点A的坐标，然后得出OB、OC、OA和AB的长度，得出△OBC为等腰直角三角形，则∠OBC=45°，CB的长度为3
，然后得出△AEC和△AFP相似得出PF的长度，从而得出点P的坐标；
（3）作点A（1,0）关于y轴的对称点A′，根据等腰直角三角形的性质得出角度．
解：（1）∵y=kx沿y轴向上平移3个单位长度后经过y轴上的点C，∴C（0，3）．
设直线BC的解析式为y=kx+3．
∵B（3，0）在直线BC上，∴3k+3=0．
解得k=－1，直线BC的解析式为y=－x+3．
∵抛物线
过点
，
解得
∴抛物线的解析式为．
（2）由． 可得D（2，－1），A（1，0）．
∴OB=3，OC=3，OA=1，AB=2．
可得△OBC是等腰直角三角形．∴∠OBC=45°，CB=3．
如图，设抛物线对称轴与x轴交于点F，∴AF=
AB=1．
过点A作AE于点E．∴∠AEB=90°．可得BE=AE=，CE=2．
在△AEC与△AFP中，∠AEC=∠AFP=90°，∠ACE=∠APF，
．
，
．解得PF=2．
∵点P在抛物线的对称轴上，
∴点P的坐标为（2,2）或（2，－2）．
（3）作点A（1,0）关于y轴的对称点A′，则A′（-1，0）
连结A′C，A′D，可得A′C=AC=
，∠OC A′=∠OCA
由勾股定理可得CD2=20， A′D2=10，
又 A′C2=10 ∴ A′D2+ A′C2=CD2
∴△ A′DC是等腰直角三角形，∠C A′D=90，
∴∠DC A′=45，∴∠OC A′+∠OCD=45，
∴∠OCA+∠OCD=45，
即∠OCA与∠OCD两角和的度数为45．
