Question

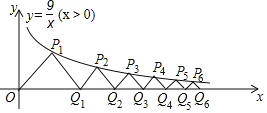
【题目】如图，在平面直角坐标系xOy中，点P1（x1，y1）、P2（x2，y2）、P3（x3，y3），……，Pn（xn，yn）均在反比例函数y＝（x＞0）的图象上，点Q1、Q2、Q3、……、Qn均在x轴的正半轴上，且△OP1Q1、△Q1P2Q2、△Q2P3Q3、…、△Qn﹣1PnQn均为等腰直角三角形，OQ1、Q1Q2、Q2Q3、……、Qn﹣1Qn分别为以上等腰直角三角形的底边，则y1+y2+y3+…+y2019的值等于_____．

Answer 1

【答案】

【解析】

过点Pn分别向x轴作垂线，交x轴于点Hn，构造等腰直角三角形，利用反比例函数建立方程，可求出y1，y2，…，从而找出规律即可．

如图，过点Pn分别向x轴作垂线，交x轴于点Hn，

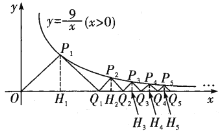
∵点Pn．在反比例函数y＝（x＞0）的图象上，且构造成等腰直角三角形，

∴，

∴OH1＝3，

∴OQ1=6，

令P2H2=y2，则有y2（6+y2）=9，

解得（舍去），，

则

，

解得，

则，

根据规律可得

故答案为.