题目内容
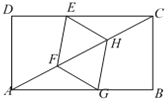
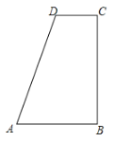
【题目】如图,在四边形ABCD中,![]() ,AB>CD,AD=AB+CD.
,AB>CD,AD=AB+CD.
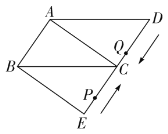
(1)利用尺规作![]() ADC的平分线DE,交BC于点E,在AD上截取AF=AB,连接AE,EF(保留作图痕迹,不写作法);
ADC的平分线DE,交BC于点E,在AD上截取AF=AB,连接AE,EF(保留作图痕迹,不写作法);
(2)在(1)的条件下,证明:EC=EF;AE⊥DE
【答案】(1)见解析;(2)证明见解析;证明见解析.
【解析】
(1)根据角平分线画法作图即可;(2)①利用条件证得△CDE≌△FDE即可;②先证得Rt△AFE≌Rt△ABE,然后利用等角代换与平行线证明与性质,即可得证
(1)如图所示;
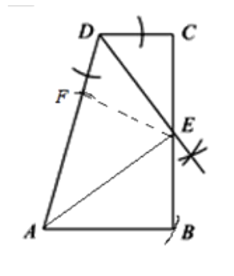
(2)证明:∵DE评分∠ADC
∴∠1=∠2
∵AD=AB+CD,AF=AB
∴DF=CD
在△CDE和△DEF中
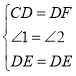
∴△CDE≌△FDE
∴CE=EF
∵△CDE≌△FDE
∴∠C=∠3=90°
∴∠4=90°
∴∠4=∠B=![]() ∠ADB
∠ADB
在Rt△AFE和Rt△ABE中
![]()
∴Rt△AFE≌Rt△ABE
∴∠5=∠6=![]() ∠BAD
∠BAD
∵∠C=∠B=90°
∴∠C+∠B=180°
∴DC∥AB
∴∠BAD+∠ADB=180°
∴∠2+∠5=90°
∴∠DEB=90°
∴AE⊥DE

练习册系列答案
相关题目