题目内容
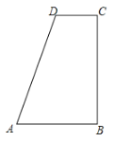
【题目】如图,在平行四边形![]() 中,
中,![]() ,以B为顶点,作
,以B为顶点,作![]() 交
交![]() 延长线于点E.
延长线于点E.
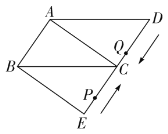
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若![]() ,
,![]() ,点P从点E出发,沿
,点P从点E出发,沿![]() 方向,以每秒1个单位的速度向终点B运动;点Q从点D出发,沿
方向,以每秒1个单位的速度向终点B运动;点Q从点D出发,沿![]() 方向,以每秒2个单位的速度向终点A运动,两点同时出发,其中一点到达终点后,另一点随之停止运动.设运动时间为
方向,以每秒2个单位的速度向终点A运动,两点同时出发,其中一点到达终点后,另一点随之停止运动.设运动时间为![]() .
.
①若![]() 是等腰三角形,求t的值;
是等腰三角形,求t的值;
②若![]() ,直接写出t的值.
,直接写出t的值.
【答案】(1)详见解析;(2)①t的值为2或0或![]() ;②
;②![]() .
.
【解析】
(1)根据有一个角是直角的平行四边形是矩形判定;
(2)①分(ⅰ)当![]() ,(ⅱ)当
,(ⅱ)当![]() ,(ⅲ)当
,(ⅲ)当![]() 三种情况,列出含t的等式,即可求出t的值;
三种情况,列出含t的等式,即可求出t的值;
②根据题意判定可得只有点P在![]() 上,点Q在
上,点Q在![]() 上时,
上时,![]() ,设PQ与BC的交点为N,证明
,设PQ与BC的交点为N,证明![]() ,得出
,得出![]() ,从而解得t值.
,从而解得t值.
(1)证明:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,
,
∴四边形![]() 是矩形;
是矩形;
(2)解:①∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() .
.
∵四边形![]() 是矩形,∴
是矩形,∴![]() .
.
若![]() 是等腰三角形,则有:
是等腰三角形,则有:
(ⅰ)当![]() ,此时有
,此时有![]() ,解得
,解得![]() ;
;
(ⅱ)当![]() ,此时有
,此时有![]() ,解得
,解得![]() ;
;
(ⅲ)当![]() 时,如解图①,过点P作
时,如解图①,过点P作![]() 于点M,则
于点M,则![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
综上,若![]() 是等腰三角形,t的值为2或0或
是等腰三角形,t的值为2或0或![]() ;
;
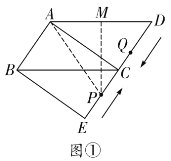

②![]() .
.
由题意可知,当![]() 时,只有点P在
时,只有点P在![]() 上,点Q在
上,点Q在![]() 上时符合题意,如解图②所示,设PQ与BC的交点为N,
上时符合题意,如解图②所示,设PQ与BC的交点为N,
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() .
.
当![]() 时,点Q在
时,点Q在![]() 上,点P在
上,点P在![]() 上,此时
上,此时![]() ,
,![]() .
.
∵四边形![]() 是矩形,∴
是矩形,∴![]() .
.
当![]() 时,有
时,有![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .∴
.∴![]() .
.
∴![]() .∴
.∴![]() .∴
.∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
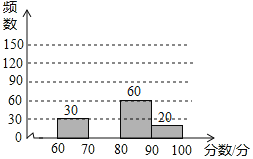
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?
【题目】某校组织“大手拉小手,义卖献爱心”活动,计划购买黑白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑 色 文化衫 | 25 | 45 |
白 色 文 化 衫 | 20 | 35 |
(1)学校购进黑.白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.