题目内容
（1）解不等式组
并把解集在数轴上表示出来；
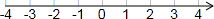
（2）如图，已知墙高AB为6.5米，将一长为6米的梯子CD斜靠在墙面，梯子与地面所成的角∠BCD=55°，此时梯子的顶端与墙顶的距离AD约为多少米？（结果精确到0.1米）（参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43）
|
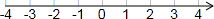
（2）如图，已知墙高AB为6.5米，将一长为6米的梯子CD斜靠在墙面，梯子与地面所成的角∠BCD=55°，此时梯子的顶端与墙顶的距离AD约为多少米？（结果精确到0.1米）（参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43）
（1）
，
解不等式①得：x≤3，
解不等式②得，x＞-1，
则不等式的解集为：-1＜x≤3，
不等式组的解集在数轴上表示为：
；
（2）在Rt△BCD中，
∵∠DBC=90°，∠BCD=55°，CD=6米，
∴BD=CD×sin∠BCD=6×sin55°≈6×0.82=4.92（米），
∴AD=AB-BD≈6.5-4.92=1.58≈1.6（米）．
答：梯子的顶端与墙顶的距离AD约为1.6米．
|
解不等式①得：x≤3，
解不等式②得，x＞-1，
则不等式的解集为：-1＜x≤3，
不等式组的解集在数轴上表示为：
；（2）在Rt△BCD中，
∵∠DBC=90°，∠BCD=55°，CD=6米，
∴BD=CD×sin∠BCD=6×sin55°≈6×0.82=4.92（米），
∴AD=AB-BD≈6.5-4.92=1.58≈1.6（米）．
答：梯子的顶端与墙顶的距离AD约为1.6米．
练习册系列答案
相关题目
______m2（结果保留根号）．
查，巡逻艇调整好航向，以26海里/小时的速度追赶，在涉嫌船只不改变航向和航速的前提下，问：
