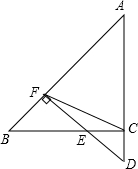
题目内容
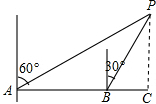
如图，在△ABC中，∠C=90°，sinB=
，F是AB上一点，过点F作DF⊥AB于F，交BC于E，交AC延长线于D，连CF，若S△BEF=4S△CDE，CE=5．
（1）求AC的长；（2）求S△CEF．
| 5 |
| 7 |
（1）求AC的长；（2）求S△CEF．
（1）∵∠BFE=∠BCD=90°，∠FEB=∠DEC
∴△BFE∽△DCE
∵S△BEF=4S△CDE，
∴S△BEF：S△DEC=4：1
∴EF：EC=2：1
∵CE=5，
∴EF=10，
∵sinB=
，
∴BE=
，
∴BC=
设AC=5k，则AB=7k
∵AB2-AC2=BC2，
∴49k2-25k2=（
）2
解得k=
（负值舍去）
∴AC=5×
=
；
（2）∵sinB=
，BE=
EF=10；∴BF=4
S△BFE=BF×EF÷2=20
∵BE：EC=
：5
∴S△CEF=
．
∴△BFE∽△DCE
∵S△BEF=4S△CDE，
∴S△BEF：S△DEC=4：1
∴EF：EC=2：1
∵CE=5，
∴EF=10，
∵sinB=
| 5 |
| 7 |
∴BE=
| 70 |
| 5 |
∴BC=
| 95 |
| 5 |
设AC=5k，则AB=7k
∵AB2-AC2=BC2，
∴49k2-25k2=（
| 95 |
| 5 |
解得k=
19
| ||
| 12 |
∴AC=5×
| 19 |
| 12 |
| 6 |
95
| ||
| 12 |
（2）∵sinB=
| 5 |
| 7 |
| 70 |
| 5 |
EF=10；∴BF=4
| 6 |
S△BFE=BF×EF÷2=20
| 6 |
∵BE：EC=
| 70 |
| 5 |
∴S△CEF=
50
| ||
| 7 |
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
