Question

沿着圆周放着一些数，如果有依次相连的4个数a，b，c，d满足不等式（a-d）（b-c）＞0，那么就可以交换b，c的位置，这称为一次操作．
（1）若圆周上依次放着数1，2，3，4，5，6，问：是否能经过有限次操作后，对圆周上任意依次相连的4个数a，b，c，d，都有（a-d）（b-c）≤0？请说明理由．
（2）若圆周上从小到大按顺时针方向依次放着2003个正整数1，2，…，2003，问：是否能经过有限次操作后，对圆周上任意依次相连的4个数a，b，c，d，都有（a-d）（b-c）≤0？请说明理由．

Answer 1

（1）答：能．
具体操作如下：

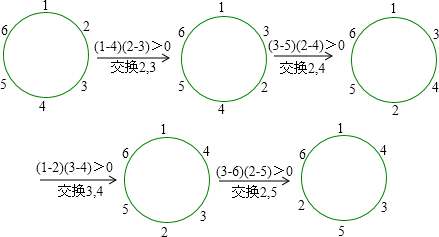
（2）答：能．
理由：设这2003个数的相邻两数乘积之和为P．
开始时，P₀=1×2+2×3+3×4+…+2002×2003+2003×1，
经过k（k≥0）次操作后，这2003个数的相邻两数乘积之和为P_k，
此时若圆周上依次相连的4个数a，b，c，d满足不等式（a-d）（b-c）＞0，即ab+cd＞ac+bd，交换b，c的位置后，
这2003个数的相邻两数乘积之和为P_k+1，有P_k+1-P_k=（ac+cb+bd）-（ab+bc+cd）=ac+bd-ab-cd＜0．
所以P_k+1-P_k≤-1，即每一次操作，相邻两数乘积的和至少减少1，
由于相邻两数乘积总大于0，
故经过有限次操作后，对任意依次相连的4个数a，b，c，d，一定有（a-d）（b-c）≤0．