��Ŀ����
����Ŀ��ֱ��������![]() �У�
�У�![]() ��ֱ��
��ֱ��![]() ����
����![]() .
.
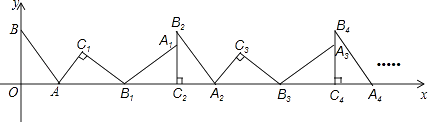
��1����![]() ʱ����ͼ1���ֱ����
ʱ����ͼ1���ֱ����![]() ��
��![]() ��
��![]() ֱ��
ֱ��![]() �ڵ�
�ڵ�![]() ��
��![]() ֱ��
ֱ��![]() �ڵ�
�ڵ�![]() .
.![]() ��
��![]() �Ƿ�ȫ�ȣ���˵�����ɣ�
�Ƿ�ȫ�ȣ���˵�����ɣ�
��2����![]() ��
��![]() ʱ����ͼ2����
ʱ����ͼ2����![]() ���
���![]() ����ֱ��
����ֱ��![]() �Գƣ�����
�Գƣ�����![]() ��
��![]() .��
.��![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ��һ�㣬�ֱ����
��һ�㣬�ֱ����![]() ��
��![]() ��
��![]() ֱ��
ֱ��![]() �ڵ�
�ڵ�![]() ��
��![]() ֱ��
ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ���������ÿ��
���������ÿ��![]() ���ٶ���
���ٶ���![]() ·���˶����յ�Ϊ
·���˶����յ�Ϊ![]() .��
.��![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ���ٶ���
���ٶ���![]() ·���˶����յ�Ϊ
·���˶����յ�Ϊ![]() .��
.��![]() ��
��![]() ͬʱ��ʼ�˶������Դﵽ��Ӧ���յ�ʱֹͣ�˶������˶�ʱ��Ϊ
ͬʱ��ʼ�˶������Դﵽ��Ӧ���յ�ʱֹͣ�˶������˶�ʱ��Ϊ![]() ��.
��.
�ٵ�![]() Ϊ����ֱ��������ʱ����
Ϊ����ֱ��������ʱ����![]() ��ֵ��
��ֵ��
�ڵ�![]() ��
��![]() ȫ��ʱ����
ȫ��ʱ����![]() ��ֵ.
��ֵ.


ͼ1 ͼ2
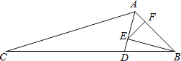
���𰸡�(1)��ACD����CBE.
(2)��![]() ��5. ����t=3.5���5���6.5��ʱ,��MDC����CEN.
��5. ����t=3.5���5���6.5��ʱ,��MDC����CEN.
��������
��1������ͬ�ǵ������ȵõ���DAC=��ECB������ȫ�������ε��ж�����֤�����ɣ�
��2���ٷֵ�N��F��C��B·���˶�����N��B��C·���˶����������������.
�ڷֵ�N��F��C·���˶�����N��C��B·���˶�����N��B��C·���˶�����N��C��F·���˶�����������㼴�ɣ�
(1)��ACD����CBE��
�������£���![]()
��![]()
��AD��ֱ��l��
��![]()
���DAC=��ECB��
����ACD����CBE��
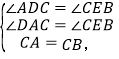
����ACD����CBE��
(2)�ٵ�![]() Ϊ����ֱ��������ʱ����N��BC�ϣ�
Ϊ����ֱ��������ʱ����N��BC�ϣ�
![]()
��![]() �ӵ�
�ӵ�![]() ������һ�ε��߶�CB��ʱ��
������һ�ε��߶�CB��ʱ��
![]()
![]()
![]() ����
����![]()
��![]() �ӵ�
�ӵ�![]() �����ڶ��ε��߶�CB��ʱ��
�����ڶ��ε��߶�CB��ʱ��
![]()
![]()
![]() ����
����![]()
��������ã�CF=BC=6cm��
��(1)���DAC=��ECB����ADC=��CEB��
�൱CM=CNʱ,��MDC����CEN��
����N��F��C·���˶�ʱ��8t=63t��
��ã�t=1���������⣬
����N��C��B·���˶�ʱ��8t=3t6��
��ã�t=3.5��
����N��B��C·���˶�ʱ��8t=3t12��
��ã�t=5��
����N��C��F·���˶�ʱ��8t=3t18��
��ã�t=6.5��
��������,��t=3.5���5���6.5��ʱ,��MDC����CEN.

 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д�����Ŀ���мס��ҡ��������ǹ���϶��ɵ�ʲ����100ǧ�ˣ����и����ǹ��ĵ��ۺ�ǧ���������ʾ���̼��ü�Ȩƽ������ȷ��ʲ���ǵĵ��ۣ�
�����ǹ� | �����ǹ� | �����ǹ� | |
������Ԫ/ǧ���� | 15 | 25 | 30 |
ǧ���� | 40 | 40 | 20 |
��1�����ʲ���ǵĵ��ۣ�
��2��Ϊ��ʹʲ���ǵĵ���ÿǧ�����ٽ���2Ԫ���̼Ҽƻ���ʲ�����м���ס��������ǹ���100ǧ�ˣ����������ɼ�������ǹ�����ǧ�ˣ�