题目内容
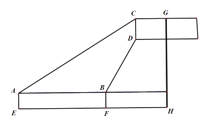
【题目】如图,在每个小正方形的边长为1的网格中,A、B均为格点.
(I).![]() 的长等于_________;
的长等于_________;
(II).请用无刻度的直尺,在如图所示的网格中求作一点![]() ,使得以
,使得以![]() 为底边的等腰三角形
为底边的等腰三角形![]() 的面积等于
的面积等于![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明);_____________
的位置是如何找到的(不要求证明);_____________

【答案】![]() 如图,取格点C,连接BC;取格点D,连接DC得点F;点G是AB与网格的交点,连接FC;取格点H,E,连接HE,线段HE交FG于点P即为所求.
如图,取格点C,连接BC;取格点D,连接DC得点F;点G是AB与网格的交点,连接FC;取格点H,E,连接HE,线段HE交FG于点P即为所求.
【解析】
(I)直接利用勾股定理即可得出答案;(II)如图,根据网格的特点取格点C,连接BC;取格点D,连接DC得点F;点G是AB与网格的交点,连接FC;取格点H,E,连接HE,线段HE交FG于点P即为所求.
(I)AB=![]() =
=![]() ,
,
(II)∵要作等腰三角形,P点须在AB的垂直平分线上,
∴取格点C,连接BC;取格点D,连接DC得点F;
根据网格的性质可知点G、F为AB、CD的中点,FG⊥AB,即,FG是AB的垂直平分线,
∵S△PAB=![]() ,AB=
,AB=![]() ,
,
∴△PAB底边AB上的高PG=![]() ,
,
∵FG=BC=AB=![]() ,
,
∴![]() ,
,
∵点G为小正方形的中点,
∴![]() ,
,
∴过格点E作AB的平行线,交FG于P,根据平行线分线段成比例定理可得点P即为所求.

故答案为:![]() ;如图,取格点C,连接BC;取格点D,连接DC得点F;点G是AB与网格的交点,连接FC;取格点H,E,连接HE,线段HE交FG于点P即为所求.
;如图,取格点C,连接BC;取格点D,连接DC得点F;点G是AB与网格的交点,连接FC;取格点H,E,连接HE,线段HE交FG于点P即为所求.

练习册系列答案
相关题目