题目内容
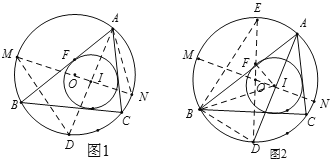
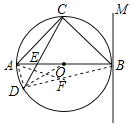
【题目】如图,![]() 是以
是以![]() 为直径的
为直径的![]() 的切线,
的切线,![]() 为切点,
为切点,![]() 平分
平分![]() ,弦
,弦![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
(1)求证:![]() 是等腰直角三角形;
是等腰直角三角形;
(2)求证:![]() ;
;
(3)求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)由切线的性质和圆周角定理可得∠ACB=∠ABM=90°,由角平分线的性质可得∠CAB=∠CBA=45°;
(2)通过证明△EDO∽△ODC,可得![]() ,即可得结论;
,即可得结论;
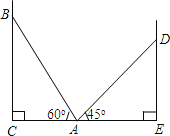
(3)连接BD,AD,DO,作∠BAF=∠DBA,交BD于点F,由外角的性质可得∠CAB=∠CDB=45°=∠EDO+∠ODB=3∠ODB,可求∠ODB=15°=∠OBD,由直角三角形的性质可得BD=DF+BF=
![]() AD+2AD,即可求tan∠ACD的值.
AD+2AD,即可求tan∠ACD的值.
证明:(1)∵![]() 是以
是以![]() 为直径的
为直径的![]() 的切线,
的切线,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]()
∵![]() 是直径
是直径
∴![]() ,
,
∴![]()
∴![]()
∴![]() 是等腰直角三角形;
是等腰直角三角形;
(2)如图,连接![]()

∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
(2)如图,连接![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∵![]()
∴![]()
∵![]() 是直径
是直径
∴![]()
∴![]()
∴![]()
∴![]()

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
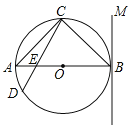
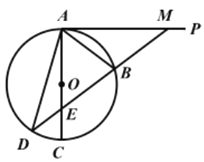
单元加期末复习先锋大考卷系列答案【题目】如图,AC是⊙O的一条弦,AP是⊙O的切线。作BM=AB并与AP交于点M,延长MB交AC于点E,交⊙O于点D,连接AD.
(1)求证:AB=BE;
(2)若⊙O的半径R=5,AB=6,求AD的长.
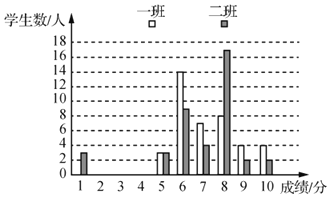
【题目】8年级某老师对一、二班学生阅读水平进行测试,并将成绩进行了统计,绘制了如下图表(得分为整数,满分为10分,成绩大于或等于6分为合格,成绩大于或等于9分为优秀).
平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 | |
一班 | 7.2 | 2.11 | 7 | 6 | 92.5% | 20% |
二班 | 6.85 | 4.28 | 8 | 8 | 85% | 10% |
根据图表信息,回答问题:
(1)用方差推断, 班的成绩波动较大;用优秀率和合格率推断, 班的阅读水平更好些;
(2)甲同学用平均分推断,一班阅读水平更好些;乙同学用中位数或众数推断,二班阅读水平更好些.你认为谁的推断比较科学合理,更客观些.为什么?