题目内容
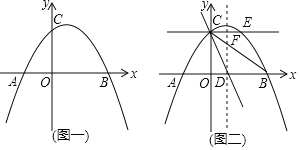
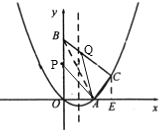
【题目】如图,在平面直角坐标系中,抛物线![]() 经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).
经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).
(I).求抛物线的解析式及它的对称轴;
(Ⅱ)点![]() 在线段OB上,点Q在线段BC上,若
在线段OB上,点Q在线段BC上,若![]() ,且
,且![]() ,求n的值;
,求n的值;
(Ⅲ)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三形?若存在,求出点M的坐标;若不存在,请说明理由.

【答案】(Ⅰ)![]() ;对称轴为直线
;对称轴为直线![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)点M的坐标为
;(Ⅲ)点M的坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(Ⅰ)利用待定系数法求出抛物线解析式即可,根据x=-![]() 得出对称轴即可;(Ⅱ)把C(m,4)代入解析式求出m的值,可得C点坐标,过C作
得出对称轴即可;(Ⅱ)把C(m,4)代入解析式求出m的值,可得C点坐标,过C作![]() 轴,垂足为E,连接AB.根据勾股定理求出AC2、BC2、AB2,根据勾股定理逆定理可得∠BCA=90°,利用HL可证明
轴,垂足为E,连接AB.根据勾股定理求出AC2、BC2、AB2,根据勾股定理逆定理可得∠BCA=90°,利用HL可证明![]() ,即可得出OP=CQ,根据OP=2BQ列方程求出n的值即可;(Ⅲ)分别讨论AB=AM、BM=BA、MA=MB三种情况,设点M的坐标为
,即可得出OP=CQ,根据OP=2BQ列方程求出n的值即可;(Ⅲ)分别讨论AB=AM、BM=BA、MA=MB三种情况,设点M的坐标为![]() ,利用勾股定理列方程求出t的值即可.
,利用勾股定理列方程求出t的值即可.
(Ⅰ)∵抛物线经过原点O,
∴抛物线解析式为![]() .
.
∵抛物线与x轴交于点(5,0),
∴![]() ,解得
,解得![]() .
.
∴抛物线解析式为![]() .
.
 ,
,
∴抛物线的对称轴为直线![]() .
.
(Ⅱ)∵点C在抛物线![]() 上,
上,
∴![]() ,解得
,解得![]() (舍),
(舍),![]() .
.
∴点C坐标为(8,4).
过C作![]() 轴,垂足为E,连接AB.
轴,垂足为E,连接AB.
在![]() 中,
中,![]() .
.
同理,可求得![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,
解得![]() .
.
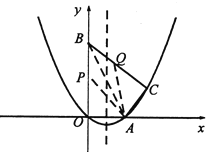
(Ⅲ)∵抛物线的对称轴为![]() ,
,
∴设点M的坐标为![]() .
.
①当![]() ,
,![]() 为顶角时,
为顶角时,
![]() ,解得
,解得![]() .
.
②当![]() ,
,![]() 为顶角时,
为顶角时,
![]() ,解得
,解得![]() .
.
③当![]() ,
,![]() 为顶角时,
为顶角时,
![]() ,解得
,解得![]() .
.
此时点![]() 为AB的中点,与点A,B不构成三角形.
为AB的中点,与点A,B不构成三角形.
综上可得,点M的坐标为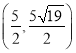 ,
,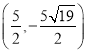 ,
,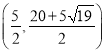 ,
,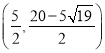 .
.

【题目】一辆汽车油箱中有汽油![]() .如果不再加油,那么油箱中的油量
.如果不再加油,那么油箱中的油量![]() (单位:
(单位:![]() )随行驶路程
)随行驶路程![]() (单位:
(单位:![]() )的增加而减少.已知该汽车平均耗油量为
)的增加而减少.已知该汽车平均耗油量为![]() .
.
(Ⅰ)计算并填写下表:
| 10 | 100 | 300 | … |
| … |
(Ⅱ)写出表示![]() 与
与![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,
,![]() 两地的路程约有
两地的路程约有![]() ,当油箱中油量少于
,当油箱中油量少于![]() 时,汽车会自动报警,则这辆汽车在由
时,汽车会自动报警,则这辆汽车在由![]() 地到
地到![]() 地,再由
地,再由![]() 地返回
地返回![]() 地的往返途中,汽车是否会报警?请说明理由.
地的往返途中,汽车是否会报警?请说明理由.