题目内容
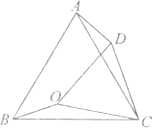
【题目】如图，点
是等边三角形
内的一点，
，将
绕点
按顺时针旋转
得到
，则下列结论不正确的是( )
A. 
B. 
C. 
D. 
【答案】D
【解析】
根据旋转的性质逐一判断即可.
∵将△BCO绕点C按顺时针旋转
得到△ACD，
∴BO=AD，故A正确，
∵OC与CD是对应边，C为旋转中心，
∴∠DOC等于旋转角，即∠DOC=60°，故B正确，
∵OC=CD，∠DOC=60°，
∴△OCD是等边三角形，
∴∠ODC=60°，
∵∠BOC与∠ADC是对应角，
∴∠ADC=150°，
∴∠ODA=150°-60°=90°，即OD⊥AD，故C正确，
∵∠ADC=150°，
∴∠DAC<30°，
∴∠BAD<90°，
∴∠ODA+∠BAD≠180°，
∴OD与AB不平行，故D错误，
故选D.
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
【题目】每年5月份是心理健康宣传月，某中学开展以“关心他人，关爱自己”为主题的心理健康系列活动．为了解师生的心理健康状况，对全体2000名师生进行了心理测评，随机抽取20名师生的测评分数进行了以下数据的整理与
①数据收集：抽取的20名师生测评分数如下
85，82，94，72，78，89，96，98，84，65，73，54，83，76，70，85，83，63，92，90．
②数据整理：将收集的数据进行分组并评价等第：
分数x |
|
|
|
|
|
人数 | 5 | a | 5 | 2 | 1 |
等第 |
|
|
|
|
|
③数据绘制成不完整的扇形统计图：
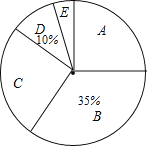
④依据统计信息回答问题
（1）统计表中的 ．
（2）心理测评等第
等的师生人数所占扇形的圆心角度数为 ．
（3）学校决定对
等的师生进行团队心理辅导，请你根据数据分析结果，估计有多少师生需要参加团队心理辅导？
【题目】8年级某老师对一、二班学生阅读水平进行测试，并将成绩进行了统计，绘制了如下图表(得分为整数，满分为10分，成绩大于或等于6分为合格，成绩大于或等于9分为优秀)．
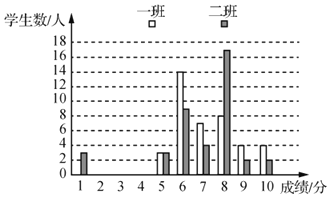
平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 | |
一班 | 7.2 | 2.11 | 7 | 6 | 92.5% | 20% |
二班 | 6.85 | 4.28 | 8 | 8 | 85% | 10% |
根据图表信息，回答问题：
(1)用方差推断， 班的成绩波动较大；用优秀率和合格率推断， 班的阅读水平更好些；
(2)甲同学用平均分推断，一班阅读水平更好些；乙同学用中位数或众数推断，二班阅读水平更好些．你认为谁的推断比较科学合理，更客观些．为什么？
