题目内容
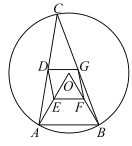
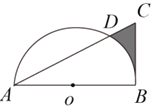
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
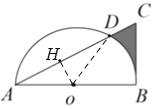
连接OD,过点O作OH⊥AC,垂足为 H,则有AD=2AH,∠AHO=90°,在Rt△ABC中,利用∠A的正切值求出∠A=30°,继而可求得OH、AH长,根据圆周角定理可求得∠BOC =60°,然后根据S阴影=S△ABC-S△AOD-S扇形BOD进行计算即可.
连接OD,过点O作OH⊥AC,垂足为 H,
则有AD=2AH,∠AHO=90°,
在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,tan∠A=
,BC=2,tan∠A=![]() ,
,
∴∠A=30°,
∴OH=![]() OA=
OA=![]() ,AH=AOcos∠A=
,AH=AOcos∠A=![]() ,∠BOC=2∠A=60°,
,∠BOC=2∠A=60°,
∴AD=2AH=![]() ,
,
∴S阴影=S△ABC-S△AOD-S扇形BOD=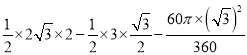 =
=![]() ,
,
故选A.

练习册系列答案
相关题目